Sector Circular
En esta página definimos sector circular y proporcionamos las fórmulas para calcular el área (en ángulos, en radianes y en función del arco) y el perímetro.
Definición
Un sector circular es la porción de un circulo delimitada por dos radios R y un arco de circunferencia L:
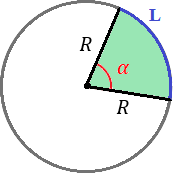 El ángulo α es el ángulo que hay entre los dos radios del sector (amplitud del ángulo central del sector).
Si el ángulo es α=2π radianes (ó 360 grados), el sector circular es un círculo completo.
El ángulo α es el ángulo que hay entre los dos radios del sector (amplitud del ángulo central del sector).
Si el ángulo es α=2π radianes (ó 360 grados), el sector circular es un círculo completo.
 El ángulo α es el ángulo que hay entre los dos radios del sector (amplitud del ángulo central del sector).
Si el ángulo es α=2π radianes (ó 360 grados), el sector circular es un círculo completo.
El ángulo α es el ángulo que hay entre los dos radios del sector (amplitud del ángulo central del sector).
Si el ángulo es α=2π radianes (ó 360 grados), el sector circular es un círculo completo.Área
Tenemos 3 fórmulas para calcular el área de un sector circular. Dos de ellas dependen del ángulo α del sector (una en grados y la otra en radianes). La otra fórmula es en función de la longitud del arco L del sector.
Fórmula del Área en grados: Para el ángulo α en grados utilizamos la fórmula
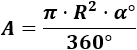 Fórmula del Área en radianes: Para el ángulo β en radianes utilizamos la fórmula
Fórmula del Área en radianes: Para el ángulo β en radianes utilizamos la fórmula
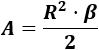 Fórmula del Área con longitud de arco: Si la longitud de arco del sector es L, entonces el área del sector es
Fórmula del Área con longitud de arco: Si la longitud de arco del sector es L, entonces el área del sector es
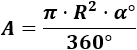 Fórmula del Área en radianes: Para el ángulo β en radianes utilizamos la fórmula
Fórmula del Área en radianes: Para el ángulo β en radianes utilizamos la fórmula
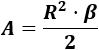 Fórmula del Área con longitud de arco: Si la longitud de arco del sector es L, entonces el área del sector es
Fórmula del Área con longitud de arco: Si la longitud de arco del sector es L, entonces el área del sector es
Perímetro
El perímetro de un sector circular es la suma de los radios R y de la longitud del arco L:
Recordatorio: la longitud del arco de circunferencia con ángulo α∘ en grados es
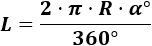 Y con ángulo β en radianes es
Y con ángulo β en radianes es
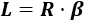
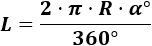 Y con ángulo β en radianes es
Y con ángulo β en radianes es
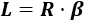
Problemas propuestos
Problema 1
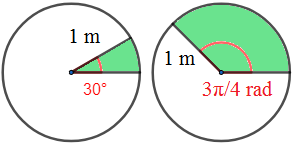 Calcular el área del sector circular de una circunferencia de radio 1 metro y ángulo
Calcular el área del sector circular de una circunferencia de radio 1 metro y ángulo
 Calcular el área del sector circular de una circunferencia de radio 1 metro y ángulo
Calcular el área del sector circular de una circunferencia de radio 1 metro y ángulo
- α=30∘
- β=3π/4 rad
Recursos:
- Arcos Circulares
- Coronas Circulares
- Áreas de figuras con formas circulares
- Problemas de Cuadrados
- Problemas de Pentágonos Regulares
- Problemas de Hexágonos Regulares
- Calculadoras de Pentágonos
- Calculadoras de Hexágonos
- Calculadoras de Circunferencias, arcos, sectores y coronas
- Áreas de Triángulos
- Problemas de trigonometría (seno y coseno)
- Teorema de Pitágoras
- Ejercicios interactivos de Geometría 2D
- Matesfacil.com