Simulationsprogramm zum Einzelspaltexperiment mit großen Anzahl von elementaren Lichtwellen. b/λ=20.
Als eindimensionale Quelle-Spalt Breite b genommen System elementaren harmonischen Emitter. Die Dichte dieser Strahler kann variieren. Mithilfe des Überlagerungsprinzips und der Vektordiagrammmethode wird das entstehende Interferenzfeld des Bildes berechnet.
Berücksichtigt die Änderung des elementaren Emitter-Feldes. Basierend auf der Physik des Phänomens sollte offensichtlich die Intensität des Lichtfeldes in der Nähe des Spaltes (Bereich der geometrischen Optik und Bereich des nahen Fresnel-Feldes) relativ zu einem bestimmten Wert oszillieren. Bei einer signifikanten Entfernung von der Quelle sollte die Intensität abnehmen. Genau dieses Verhalten der Schwingungsintensität kann erreicht werden, wenn die Amplitude der sekundären elementaren Wellen mit der Entfernung r nach dem Gesetz abnimmt: 1/sqrt(r) für eindimensionale und 1/r-für ein zweidimensionales Modell.
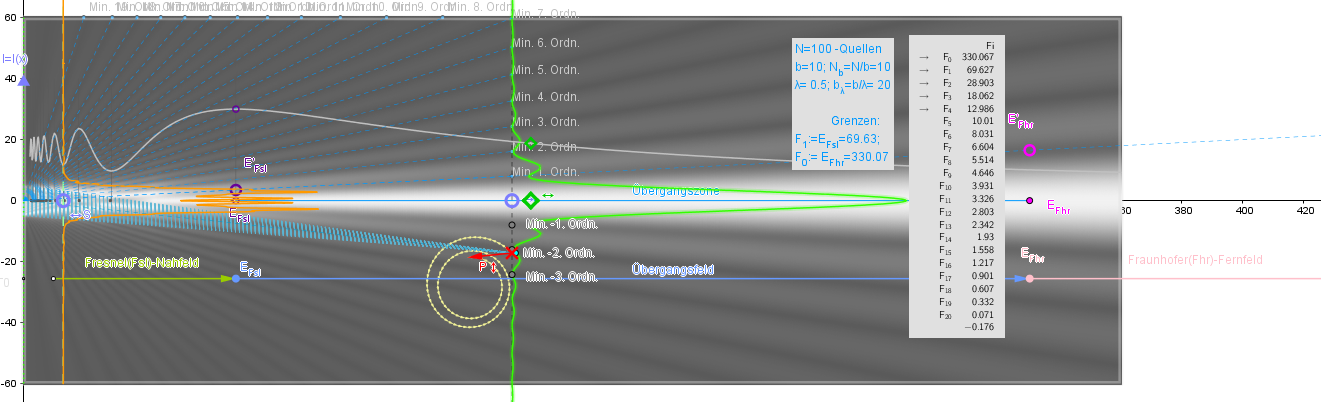
Die Intensität des Feldes auf der Achse des Spaltes. Das Applet zeigt diese Abhängigkeit in einem Fall von der Entfernung vom Spalt x(rechte Teil des Applets) und in einem anderen(linke Teil des Applets) - von dem Fresnel v Parameter →v:=b/sqrt (2 λ x). Wenn Sie die Beugungseinstellungen ändern, klicken Sie die "Max.Sync-Taste", die sich im linken Teil des Applets befindet. In diesem Fall wird das Maximum der ersten Peak der dargestellten Abhängigkeit oder das letzte Maximum F1 auf der rechten Abhängigkeit berechnet. Die restlichen Extrempunkte werden (mit dem Fresnel-Zonen-Schema für kreisrunden Öffnung) gefunden. Diese Brennpunkte auf der Spaltenachse werden als F1, F2, ... bezeichnet. Entdecken Sie die Auswirkungen der Anzahl der elementaren Strahler auf die Ergebnisse!
Bereiche der Beugung. Die Intensitätsverteilung auf der horizontalen Achse, senkrecht zur Spaltachse und durch den Brennpunkt F1, weist charakteristische Schwingungen auf. Finden wir den Bereich des Interferenzfeldes, nämlich den Punkt F0, wo die Amplitude des Feldes des ersten Interferenzminimums um den Faktor e = 9 gegenüber seinem Wert für die Abhängigkeit im Abstand F1 abnimmt. Wir betrachten den Bereich des Beugungsbildes bis F1 -als Nahfeldbereich (Fresnel-Beugung), hinter dem F0 -als Fernfeldbereich (Fraunhofer-Beugung) und zwischen F1 und F0 als Übergangsbereich.
Die Visualisierung des Lichtfeldes kann durch Scannen im Abschnitt Färbung der Lichtfeldverteilung durchgeführt werden. Um dies zu tun, müssen Sie die Scanpunkte mit der Schaltfläche "Execute"(taste klicken) erstellen und scanen. Klicken Sie auf die Schaltfläche "Heatmap" bλ =20 und Sie können das bereits vorhandene Bild des Interferenzfeldes verwenden.

Weitere detaillierte Bilder zu diesem Applet finden Sie in https://www.geogebra.org/m/s3xcxme2. Applet für den Fall bλ =10 finden Sie in https://www.geogebra.org/m/dyw3j8e2.