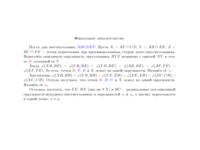
Доказательство т. Паскаля через радикальные оси
Как можно доказать теорему Паскаля
Теорема Паскаля — одна из первых теорем, которые я проходил, которая была не про изъезженные вдоль и поперёк треугольник или четырёхугольник, а ШЕСТИугольник.
Звучит она так*: если во вписанном шестиугольнике пересечь попарно противоположные стороны, то три такие точки пересечения будут лежать на одной прямой.
Первое доказательство, которое я узнал, было через дополнительные построения, вписанные углы и гомотетичные треугольники. Потом я узнал доказательство через сведение с помощью полярного преобразования теоремы Паскаля к теореме Брианшона (а у последней есть ряд своих доказательств, в частности, через радикальные оси), через частный случай теоремы о девяти точках на кубике, через изогональное сопряжение. В конце концов её можно решить с помощью моего любимого метода: двигать точки и смотреть на двойные отношения.
Большинство этих решений были какие-то "сложные" или работали нормально только в частных случаях.
И тут, недавно у меня на уроке частный случай этой теоремы доказал Рябов Егор. Причём доказал через какие-то элементарнейшие углы и радикальные оси. То есть такие две темы, которые знает и понимает каждый школьник, который хоть чуть-чуть занимался олимпиадной геометрией.
Собственно, для понимания доказательства вроде достаточно картинки и знания, что точку R мы определяем как пересечение оранжевой окружности и прямой XY.
Теорема Паскаля
Формальное доказательство теоремы Паскаля через радикальные оси
Примечания
*В совсем общем случае, конечно, теорема Паскаля формулируется не для шестиугольника, вписанного в окружность, а для шести точек на конике.
Но проективным преобразованием конику можно перевести в окружность, а расположением точек на окружности за счёт использования ориентированных углов мы не пользовались.
Конечно, ещё бывают случаи совпадения точек (и там тоже за счёт ориентированных углов всё должно быть хорошо) и бывает, что прямые не пересекаются в одной точке, а параллельны.