Intersecting Circles and Limits
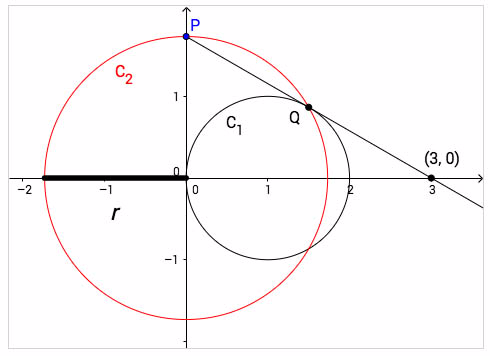
Making a Prediction
What will happen to the point (, 0) as approaches zero? Explain your reasoning.
Coming up with a Plan
Now that we've made a prediction, let's see if we can prove what will happen to the point. Come up with a plan. How can we prove what will happen to the point (, 0) as the radius decreases to zero?
Part 1: Identifying Preliminary Information
To determine what happens to the point (, 0), we need to find the equation of line . In order to do this, we must identify the coordinates of points and . What are the coordinates of point ?
Circle 1
In order to find the coordinates of point we must identify the equation of each circle. Which equation describes circle ?
Circle 2
Which equation describes circle ?
Part 2: Using a System of Equations
Finding the x-coordinate
What is the x-coordinate of the intersection point? Use the hints below if you get stuck.
Hints
Finding the y-coordinate
Now that we have the x-coordinate of the intersection point, we can find the y-coordinate. Substitute the x-value back into either equation and solve for y. What is the y-coordinate of the intersection point? Use the hints below if you get stuck.
Hints
The Coordinates of Point Q
Part 3: Using the Equation of PQ
Since we have the coordinates of points P and Q, we can identify the slope of the line. The slope between any two points can be found using the formula Which expression represents the slope between the two points? Use the hints below if you get stuck.
Hints
Writing and Solving an Equation
Now that we have identified the slope of line PQ, we can write an equation that describes it. Since we are interested in identifying the value of , substitute y = 0 into the equation and solve it for . Which equation describes ? Use the hints below if you get stuck.
Hints
Part 4: Finding the Limit
Now that we have an expression for in terms of , we can evaluate its limit as approaches zero: Note that direct substitution in this instance fails, resulting in indeterminate form: Our expression for contains a removable discontinuity. There are multiple ways we can address this. Without using calculus, we can evaluate this limit by rationalizing the denominator, using the conjugate method. After rationalizing the denominator and simplifying the result, which of the following represents the same value as the original limit? Use the hints below if you get stuck.
Hints
Evaluating the Limit
Now that we have removed the discontinuity, we can evaluate the limit and find the result we were looking for. What is the result of evaluating the limit? Use the hints below if you get stuck.
Hints
Part 5: Reflecion
Was your prediction correct? Were you surprised by the results?
Visualizing the Results
Part 6: Calculus Extension
Before rationalizing the denominator in our limit expression we had the following: Another way to evaluate this limit is by using L'Hôpital's Rule. This rule states that to evaluate a limit that results in indeterminate form, differentiate the numerator and differentiate the denominator, and then evaluate the resulting limit. Using L'Hôpital's Rule and the Chain Rule, evaluate the limit. Click "Check" at the bottom of the page to verify all of your results.