Side-Side-Side
SSS Illustrated
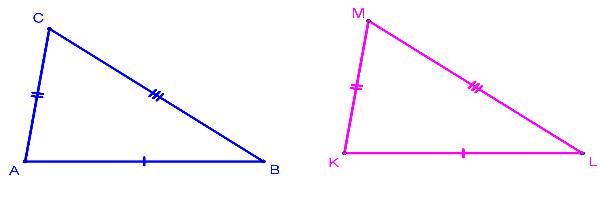
SSS Explained
If three sides of a triangle are congruent to three sides of another triangle, the
triangles are congruent.
Below is an example how to construct this. If you change anything in the construction, just click on the arrows on the top right to restore the construction.
Example:Constructing SSS
Steps in constructing SSS
Now you try to draw a triangle congruent to the previous one You need to draw a triangle with three sides: AB=5cm, AC=7cm and BC=8 cm. Try to do this in the "Applet" below
- Use
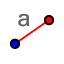to draw segment AB and if you are requested to give the length type in 5
- Use
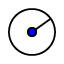click on point A and then when requested to provide the radius type in 7
- Use
click on point B and then when requested to provide the radius type in 8
- Use
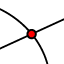to plot point C at the intersection of the two circles
- Use
and click on point A, B and C to create the triangle
Your attempt to construct SSS
Exploring SSS
Pythagorean Triples
Read more about Pythagorean Triples by clicking here: