GeoGebra Lab #2: Geometry in the World
In this GeoGebra lab, you will become more familiar with the tools provided by GeoGebra as you explore geometric objects and properties in real-world subjects.
Measuring Angles at Chimney Rock
Use the instructions below to help you measure the angle of elevation from the base to the summit of Chimney Rock in Nebraska.
(Image credit: Mike Tigas of Columbia, MO)
Instructions
 Draw the horizon line across the base of Chimney Rock. (Where the green grass meets the brown/red rock.)
Draw the horizon line across the base of Chimney Rock. (Where the green grass meets the brown/red rock.)
 Drag the right point of the horizon line to the rightmost point of the base of Chimney Rock.
Drag the right point of the horizon line to the rightmost point of the base of Chimney Rock.
 Create a point at the very top of Chimney Rock.
Create a point at the very top of Chimney Rock.
 Measure the angle of elevation by clicking the top point, then the rightmost point, then the third point along the line.
Measure the angle of elevation by clicking the top point, then the rightmost point, then the third point along the line.
 Drag the number label of the angle up into the blue sky so that you can read it.
Drag the number label of the angle up into the blue sky so that you can read it.
What is the angle of elevation of Chimney Rock, according to your construction?
Dividing a pizza into five slices
Use the instructions below to help you divide this delicious pizza into five equal slices.
Instructions
 Create a circle with a center at the middle of the pizza and radius so that the circle roughly follows the edge of the pizza.
Create a circle with a center at the middle of the pizza and radius so that the circle roughly follows the edge of the pizza.
 If necessary, drag your center and radius-point until you are satisfied with their positions.
If necessary, drag your center and radius-point until you are satisfied with their positions.
 Use the "Angle with a Given Size" tool (DIFFERENT FROM THE ANGLE MEASURE TOOL!) to create an angle whose measure is one-fifth of the size of the whole pizza. First select the point on the edge of the pizza, then the center, then type in the correct angle measure.
Use the "Angle with a Given Size" tool (DIFFERENT FROM THE ANGLE MEASURE TOOL!) to create an angle whose measure is one-fifth of the size of the whole pizza. First select the point on the edge of the pizza, then the center, then type in the correct angle measure.
 Repeat step 3 until you have 5 points along your circle.
Repeat step 3 until you have 5 points along your circle.
 Draw five line segments from the center of the pizza to the points along the edge to create your slices.
Draw five line segments from the center of the pizza to the points along the edge to create your slices.
What was the measure that you used to create one slice of pizza?
Jefferson Memorial Scavenger Hunt
Use the Parallel and Perpendicular Line tools, as described below, to find examples of parallel and perpendicular lines in the Jefferson Memorial Building.
Instructions
 Draw a line on the building to which you would like to draw parallel or perpendicular lines. (For example, you could draw a line along a column.)
Draw a line on the building to which you would like to draw parallel or perpendicular lines. (For example, you could draw a line along a column.)
 Create a point (NOT on your original line) through which you would like to draw a parallel line. (For example, a point on a different column.)
Create a point (NOT on your original line) through which you would like to draw a parallel line. (For example, a point on a different column.)
 Use the parallel line tool to draw a line parallel to your original line that also appears in the picture. (For example, a different column.) To use this tool, select the original line that you drew, then click the point you created not on the original line.
Use the parallel line tool to draw a line parallel to your original line that also appears in the picture. (For example, a different column.) To use this tool, select the original line that you drew, then click the point you created not on the original line. Create a point (NOT on your original line) through which you would like to draw a perpendicular line.
Create a point (NOT on your original line) through which you would like to draw a perpendicular line.
 Use the perpendicular line tool to draw a line perpendicular to your original line that also appears in the picture. To use this tool, select the original line that you drew, then click the other point.
Use the perpendicular line tool to draw a line perpendicular to your original line that also appears in the picture. To use this tool, select the original line that you drew, then click the other point.
 Drag your points/lines around the screen until you are confident that your parallel and perpendicular lines line up with features of the Jefferson Memorial.
Drag your points/lines around the screen until you are confident that your parallel and perpendicular lines line up with features of the Jefferson Memorial.
 Use the semicircle tool to trace a semicircle in the Jefferson Memorial. (You may have to try this more than one time to get the correct half of the circle to show up.)
Use the semicircle tool to trace a semicircle in the Jefferson Memorial. (You may have to try this more than one time to get the correct half of the circle to show up.)
How do the parallel and perpendicular line tools in GeoGebra illustrate the Parallel and Perpendicular Postulates?
Find the Center of this Monument
In this task, you will use the instructions below to find a center of the triangular monument in Gagra, Georgia.
(As we will learn in Chapter 5, there is more than one center of a triangle!)
(Image credit: Vycheslav Stepanyuchenko of Rostov-on-Don, Russian Federation)
Instructions
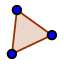 Create a triangle that follows the borders of the monument by selecting the three vertices of the triangle shape, then selecting the first vertex again. (For example, click the left point, the top point, the right point, then the left point again.)
Create a triangle that follows the borders of the monument by selecting the three vertices of the triangle shape, then selecting the first vertex again. (For example, click the left point, the top point, the right point, then the left point again.)
 Use the Perpendicular Bisector tool to bisect each of the three sides of the triangle.
Use the Perpendicular Bisector tool to bisect each of the three sides of the triangle.
 Use the intersect tool to choose the intersection of your perpendicular bisectors.
Use the intersect tool to choose the intersection of your perpendicular bisectors.
What do you notice about your three perpendicular bisectors? (Specifically, I'm asking about the point of intersection here.) Do you think this is true for all triangles, or just the special shape of this monument?