GeoGebra Lab #4: Non-Euclidean Geometry
Non-Euclidean Geometry
Spherical Geometry
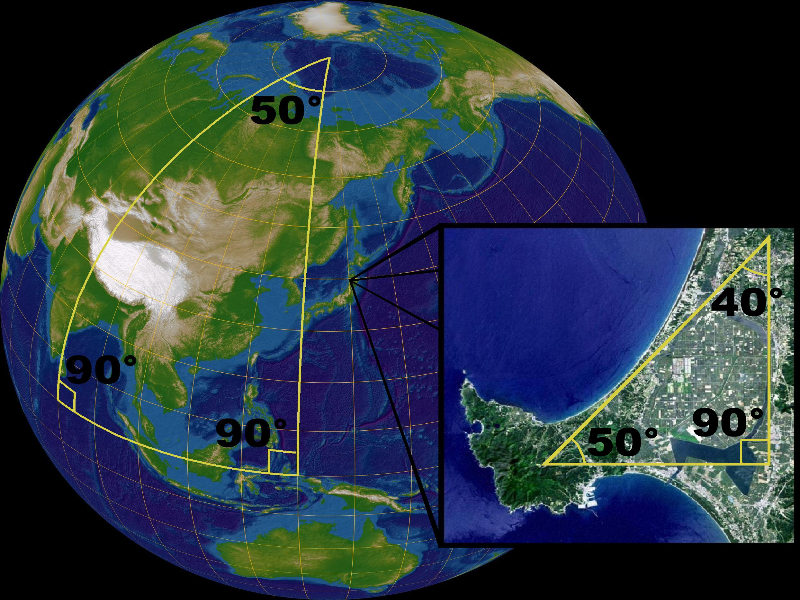
Question #1
Make a conjecture (an educated guess) about the sum of triangle measures in a triangle on a sphere.
Poincaré Disks

Question #2
Is the Parallel Postulate true in the Poincaré disk? That is, given the hyperbolic (curved) line AB and a point C in the disk not on AB, is it true that there is EXACTLY ONE hyperbolic (curved line) through C that does not intersect with AB? Experiment with the applet before you answer.
Fractal Geometry
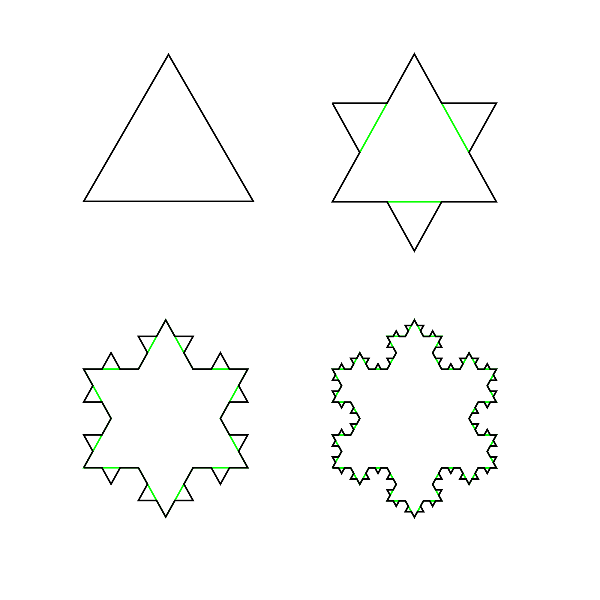
Koch snowflake

Dragon curve
Fractals in the movies
Fractals in Nature
Question #3
What's your favorite example of fractals in nature?
Sierpinski triangle
Question #4
At each stage, how many shaded-in equilateral triangles are there? (Your answer should include four numbers, one for each of Stage 0 - Stage 3.) How many triangles will there be at Stage n? (That is, find a formula in terms of the variable n that represents the number of shaded triangles at each Stage.)
Question #5
Suppose that the area of the original (Stage 0) triangle is 1 square unit. What's the area of each smaller component triangle in each subsequent stage? (For example, the area of one shaded triangle in Stage 1 is 1/4.) What will the area of one small shaded triangle be at Stage n? (That is, find a formula for the area of one small triangle, in terms of n.)
Question #6
What is the total shaded area at each stage in the Sierpinski triangle? What will the total shaded area be at Stage n? (That is, find a formula for the total shaded area in terms of n.)