le isometrie inverse (o invertenti)- coniugazione seguita da roto-traslazione: se, prima di eseguire una roto-traslazione, si esegue un ribaltamento intorno all'asse reale (ossia la isometria conj), si ottiene quel che si chiama una isometria inversa (o invertente). Pertanto, una isometria inversa è una trasformazione del tipo: Tv
 Ruconj con u U e vC
- le isometrie inverse e la sovrapponibilità di figure piane uscendo dal piano: se una figura F viene trasformata nella figura F' da un'isometria invertente, si ha che F e F' sono della stessa forma e grandezza, ma non è possibile portare F a sovrapporsi a F' se non uscendo dal piano
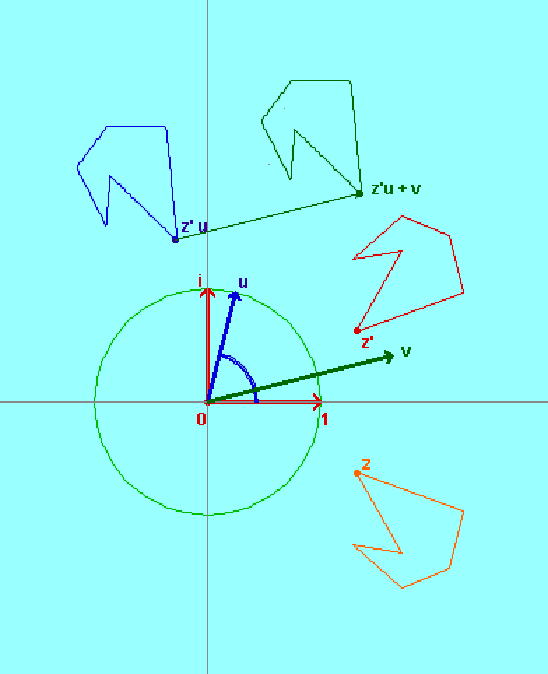
- formula di un'isometria inversa: ricaviamo subito, dalla definizione: (TvRuconj)(z) = u•z + v
- roto-traslazione seguita da coniugazione: se la coniugazione si opera dopo la roto-traslazione si ha:
(conjTvRu)(z) = u•z + v = u•z + v = u•z + v = (T vRu)(z), ossia: conj Tv Ru = T v Ru conj
- proprietà delle isometrie inverse:
- composizione di isometrie inverse: la composta di due isometrie inverse è una isometria diretta. Infatti:
(Tv'Ru'conj) (TvRuconj) = (Tv'Ru'conj) (conjTv Ru) = (Tv'Ru') (Tv Ru) e quest'ultima è la composta di due roto-traslazioni e quindi, come visto, è una roto-traslazione
- coniugazione e altri ribaltamenti: la coniugazione è una isometria inversa, in quanto conj = idconj (e l'identità è una isometria diretta). E' però più interessante osservare che se si vuol ribaltare un punto z non intorno all'asse reale, ma intorno a una generica retta contenente un punto unitario u, basta ruotare z con la rotazione R1/u=Ru (che porta u in 1), poi effettuare la coniugazione, e infine ruotare con la rotazione Ru (che porta 1 in u). Si ottiene così la cosiddetta simmetria assiale intorno alla retta Ru, data dalla formula: Su := Ru conj R1/u.
Anche questa trasformazione è una isometria invertente (provarlo come esercizio)
- inversione di una isometria invertente: l'isometria invertente TvRuconj ha come trasformazione inversa l'isometria invertente conjR1/uT-v
- inversione dell'orientamento: dati tre punti A, B, C e una isometria invertente che li porti rispettivamente in A', B', C', i percorsi ABC e A'B'C' sono uno orario e l'altro antiorario, oppure uno antiorario e l'altro orario (brevemente si dice che sono discordi). In effetti basta osservare che questo scambio di versi di percorrenza è effettuato da conj e che la componente rototraslativa di una isometria invertente non fa altro che mantenere il verso che conj ha invertito.
|
