More triangle centres...

Part 1

The altitude of a triangle is constructed by drawing a line from a vertex of the triangle to the opposite side such that the line is perpendicular to the side.

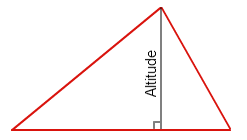
Question 1

Construct the altitudes for the triangle shown below.

Question 2

i. What do you notice about the three altitudes you constructed? ii. Does it make any difference when you drag any of the vertices of the triangle?

Question 3

i. In your notebook, show how to demonstrate ANALYTICALLY what you described about the relationship between the altitudes of a triangle. Use the example of a triangle with vertices at (1, 6), (11, 4) and (2, -2) to help you do this. ii. Using the diagram below, check your result.

Question 4

Using the diagram below: i. Construct a triangle, ABC. ii. Construct the altitudes of triangle ABC. iii. Through each of the vertices of the triangle construct a line parallel to the opposite side of the triangle to form triangle PQR. Where A lies on RQ and B lies on PR.

Question 5

i. Explain why RA = BC..? ii. Which other line segment is equal to BC..? iii. What conclusion can you come to from your results above?

Question 6

i. How would you describe the relationship between AE and RQ, and why? (Note: E lies on BC and D lies on AC, etc) ii. Which other pairs of lines have the same relationship? iii. What can you say about the relationship between the ALTITUDES, AE, BD and CF in relation to triangle PQR? iii. Hence, what can say about the relationship between the ALTITUDES, AE, BD and CF of triangle ABC that proves what you described in Question 2.