How long is the Brittish Coast?
How long is the circumference of a rectangle
One can measure the lenght of the circumference of a rectangle with segments of equal length.
When clicking on the button measure with length 2, you see that the circumference equals 16 segments.
The length of it becomes: 16 x 2 = 32.
We now do the same for the coast of Great Brittain.
Explain your observations.
Benoit Mandelbrot asked himself: "How long is the Brittish coast??"
A simple question, it seems. For he could find it in any encyclopedia.
The curious thing is that the data he found were very diverse.
Mandelbrot discovered that the length depends of the unity of measurement.
While measuring the circumference of a rectangle, the unity of measurement doesn't matter, but for the length of the Brittish coast it was essential.
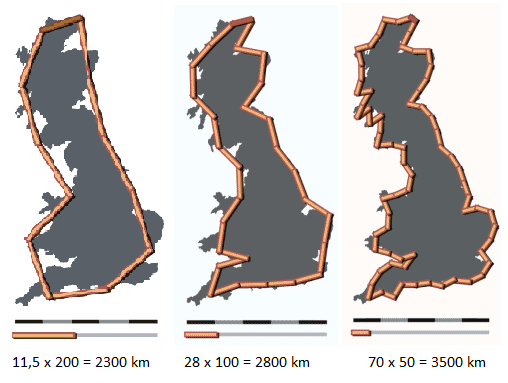
Using a ruler of 200 km, it's very difficult to measure the irregular form of the coast.
You can do a lot better with a ruler of 100 km, and still better with one of 50 km.
The smaller the rulers become, the larger the coastline becomes.
You would think that one approaches the 'right' length better and better, while using smaller rulers.
But on the contrary the lenght keeps on becoming larger and larger, up to infinity although it's limited.
Mandelbrot concludes that the coastline must have a dimension between 1 and 2.
It's remarkable that while zooming the factor of increment of the length always equals the zoomfactor: 1,25.
This proportion he called the fractal dimension of the coastline.
This fractal dimension rates the irregularity of the coast.
Every coast seems tho have its own dimension, e.g. for the very irregular westcoast of Ireland one finds 1,26 when the smoother eastcoast has but a dimension of 1,10 and the rough Norwegian fjords even reach a dimension of 1,52.
This new way of looking unto nature gave birth to a new geometrical concept: a fractal.
- A fractal is self-similar: when you zoom in the result looks the same as the original. Details show the same irregularity as the total view.
- A fractal has got a fractal dimension, which is not necessary an integer.