Bewijs voor de som van veelhoeken
geheel is som van de delen
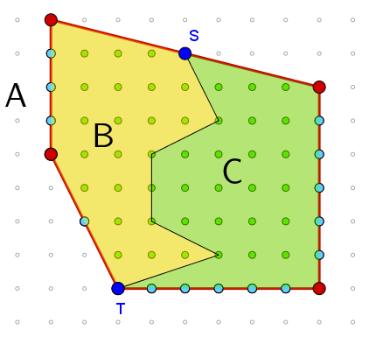
Een roosterveelhoek A is opgesplitst in twee roosterveelhoeken B en C. De som van de oppervlakten van deze twee veelhoeken is uiteraard gelijk aan de oppervlakte van de grote veelhoek. Maar hoe zit het met de Pickgetallen van B en C?
benamingen
- Het aantal inwendige punten van A, B en C noemen we iA, iB en iC.
- Het aantal randpunten van A, B en C noemen we rA, rB en rC.
- Het aantal randpunten dat B en C gemeenschappelijk hebben, noemen we k.
- Tenslotte zijn er de twee punten S en T, randpunten van zowel A, B als C.
De oppervlakte van veelhoek A volgens Pick
- De inwendige punten van A zijn deze van B en C + de randpunten van B en C behalve S en T. symbolisch: iA = iB + iC + (k - 2).
- De randpunten van A zijn deze van B die geen randpunt zijn van C + deze van C die geen randpunt zijn van B + S en T. symbolisch: rA = (rB - k) + (rC - k) + 2 = rB + rC - 2k + 2