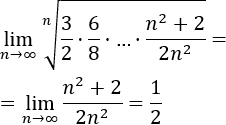Criterios de la media geométrica y de la raíz
Los límites de las sucesiones se calculan aplicando los mismos razonamientos que en los límites de las funciones, pero en ocasiones estos razonamientos no son suficientes. Es entonces cuando empleamos los criterios de convergencia específicos para sucesiones.
En esta página enunciamos el criterio de convergencia de la media geométrica y el criterio de la raíz (que es un corolario del anterior).
Criterio de la raíz
Sea una sucesión de reales positivos tal que
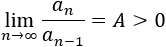 Entonces,
Entonces,
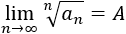 Ejemplo:
Ejemplo:
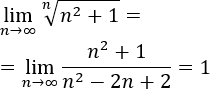 Más ejemplos: Criterio de la media geométrica y criterio de la raíz
Más ejemplos: Criterio de la media geométrica y criterio de la raíz
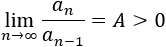 Entonces,
Entonces,
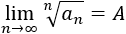 Ejemplo:
Ejemplo:
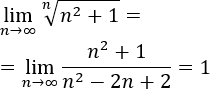 Más ejemplos: Criterio de la media geométrica y criterio de la raíz
Más ejemplos: Criterio de la media geométrica y criterio de la raízRecursos
Criterios de convergencia:
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
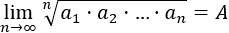 Nota: el criterio también es válido para A=+∞.
Ejemplo:
Nota: el criterio también es válido para A=+∞.
Ejemplo: