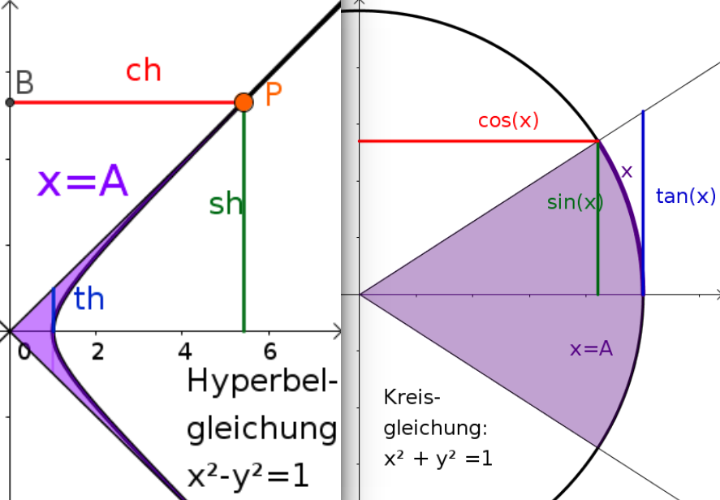
Üblicherweise erscheint als Argument in den goniometrischen Funktionen die Bogenlänge x des Winkels, weshalb diese Funktionen meist als "Winkelfunktionen" und ihre Umkehrfunktionen als "Arcusfunktionen" bezeichnet werden.
Bei den Hyperbelfunktionen ist das Argument x=A die violett gekennzeichnete Fläche (Beweis durch Integralrechnung mit Hilfe der Definitionsgleichungen!), weshalb deren Umkehrfuktionen auch "Areafunktionen" heißen.
Diese Betrachtungsweise lässt sich analog auf den Einheitskreis übertragen, wenn man mit A und x die Maßzahlen von Bogenlänge und Kreissektor bezeichnet:
, wegen r=1 folgt A=x