Gaussian Elimination
1. Introduction
A system of (linear) equations is a group of (linear) equations with various unknown factors. Generally speaking, the unknown factors appear in various equations.
What an equation with various unknown factors does is relates them amongst each other.
Solving a system consists in finding the value for the unknown factors in a way that verifies all the equations that make up the system.
- If there is a single solution (one value for each unknown factor) we will say that the system is Consistent Independent System (CIS).
- If there are various solutions (the system has infinitely many solutions), we say that the system is a Consistent Dependent System (CDS).
- If there is no solution, and this will happen if there are two or more equations that can't be verified at the same time, we say it's an Inconsistent System (IS).
2. Resolution Method
- We apply the Gauss-Jordan Elimination method: we obtain the reduced row echelon form from the augmented matrix of the equation system by performing elemental operations in rows (or columns).
- Once we have the matrix, we apply the Rouché-Capelli theorem to determine the type of system and to obtain the solution(s), that are as:
- AX = B is consistent if, and only if,
- AX = B is consistent independent if, and only if,
3. Example 1
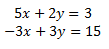The augmented matrix of the system is
of the same dimension as the system (2x3). The vertical line that separates the matrix coefficients from the vector of the independent terms.
We perform elemental operations in the rows to obtain the reduced row echelon form: We multiply the first row by 1/5 and the second by 1/3
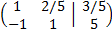
We add the second row with the first
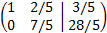
We multiply the second row by 5/7
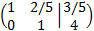
We add the first row with the second one multiplied by -2/5
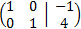
This last equivalent matrix is in the reduced row echelon form and it allows us to quickly see the rank of the coefficient matrix and the augmented one.
We calculate the ranks: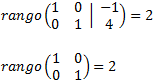
By the Rouché-Capelli theorem, the system is consistent Independent. The matrix we have obtained represents the system
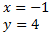
which is the solution to the initial system.