number of digits compared
Now let's compare the growth of the number of digits when taking different starts.
In following applet the number of digits is graphed for taking as start respectively 1, 2, 312 and 23.
Conway's constant
Conway found a rule that describe the grow of the number of digits:
If we write the number of digits of the n-th element as Ln , then there's a limit for the ratio given by
with =1.303577269034...
This constant λ is known as Conway's constant.
More, Conway's constant is the unique positive real root of the following polynomial of degree 71.
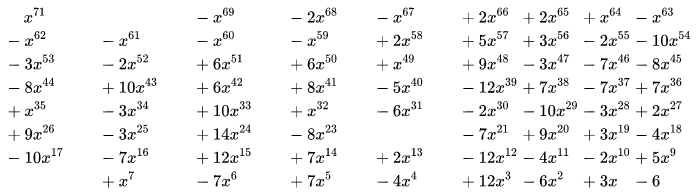
Graphed in the complex plane we see (marked in red) as the only root of the polynomial on the x-axis, where the other complex roots circle around the origin.