Relazioni e funzioni: caratteristiche di base
RELAZIONI E FUNZIONI
Definiamo una relazione tra due insiemi un qualsiasi legame tra di essi che associa ad un elemento del primo insieme uno o più elementi del secondo. Per dare un nome ad una relazione si utilizza una lettera minuscola. Facciamo un esempio.
Dati l'insieme delle lettere e quello delle parole, la relazione p: "", permette di associare ad una lettera (ad esempio "c") la parola "casa", "cattedra" o altre; alla lettera "s" verranno associate parole come "stella", "studente" e così via. Se chiamiamo il risultato della relazione, cioè l'elemento associato ad , possiamo descrivere la relazione scrivendo p : "".
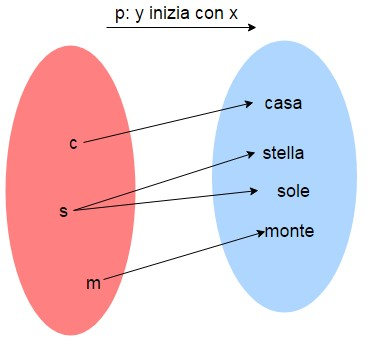
Si chiama funzione una relazione che ad ogni elemento del primo insieme associa un solo elemento del secondo insieme (quindi se ha un solo risultato). L'esempio visto sopra è una relazione ma non è una funzione, perché data una lettera esistono ovviamente più parole che iniziano con quella lettera. Se invece consideriamo la relazione i:"", mostrata qui sotto, abbiamo che ogni lettera ha una sola iniziale. La relazione i quindi è anche una funzione.
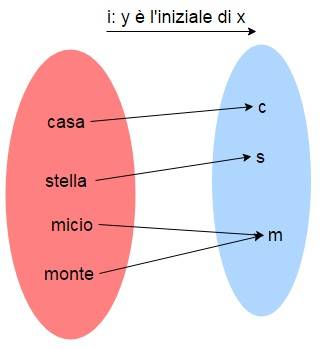
Una funzione può anche essere considerata una "relazione univoca", in quanto ad ogni elemento del primo insieme viene assegnato in modo univoco (cioè unico) l'elemento del secondo insieme. Avere una funzione, ovvero definire in maniera univoca il risultato, è particolarmente importante per le relazioni matematiche, dato che in genere è necessario che ogni operazione porti ad un solo risultato univocamente definito, cioè che sia lo stesso per chiunque stia applicando quell'operazione.
LE VARIABILI DI UNA FUNZIONE
La , cioè l'elemento preso nel primo insieme, viene chiamata variabile indipendente, perchè è un elemento che varia (nell'esempio posso considerare varie parole) e può essere scelto liberamente da chi utilizza la funzione; può anche essere considerato l'input che la funzione riceve ed a cui essa associa un output, o risultato, cioè la , il cui nome formale è variabile dipendente perché dipende appunto dalla che abbiamo scelto in partenza: una volta scelta liberamente la , la viene stabilita univocamente dalla funzione, e noi non abbiamo scelta in proposito.
Nell'esempio riportato sopra si può dire che "s" è l'output prodotto dall'input "stella" secondo la funzione i.
La che viene trovata come risultato di una certa secondo una data funzione viene anche chiamata immagine della di partenza, che per contro può essere definita come controimmagine della corrispondente.
Ad esempio "m" è l'immagine di "micio" e di "monte", che sono quindi sue controimmagini; "casa" è la controimmagine dell'output "c".
Le varie notazioni possibili per indicare le variabili di una funzione possono essere riassunte quindi nella seguente tabella:
L'insieme dei valori nell'insieme di partenza per cui la funzione genera un risultato è detto dominio (in Inglese: domain) della funzione. L'insieme dei valori nell'insieme di destinazione che sono un risultato di qualche input (cioè che sono controimmagine di almeno una è detto codominio (in Inglese: range).
FUNZIONI MATEMATICHE
Abbiamo detto che avere una funzione, ovvero definire in maniera univoca il risultato, è particolarmente importante per le relazioni matematiche, cioè tra relazioni che prendono dei numeri come input ed output. Vediamo quindi qualche esempio di relazione matematica.
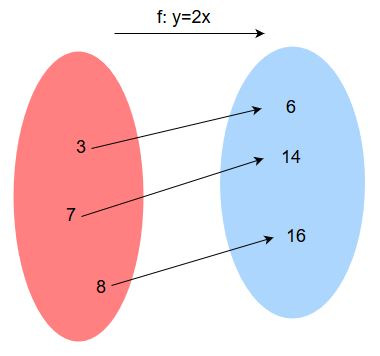
La relazione f: "" associa ad esempio al numero 3 il numero 6, a 7 associa 14 e così via. Un altro modo per descrivere questa relazione, particolarmente chiaro nel caso delle relazioni matematiche, è , che indica direttamente l'espressione (o la formula, anche se stranamente questa parola non viene usato in questo ambito) che permette di calcolare il risultato partendo dall'input .
| x | y |
| variabile indipendente | variabile dipendente |
| input | output (risultato) |
| controimmagine | immagine |
Per esprimere la relazione tra un certo valore e la corrispondente immagine (cioè il risultato) fornito dalla funzione si scrive che
Che si legge : "f di 3 è uguale a 6", che probabilmente è il modo veloce per dire "il risultato secondo la legge f dell'input 3 è uguale a 6" - cioè quando Il viene messo "dentro" la funzione (cioè sostituito alla ) e genera come risultato . Allo stesso modo possiamo scrivere . Possiamo usare questa notazione per indicare relazioni più articolate, come
- - "il risultato che si ottiene dall'input è minore di un certo numero "
- - "il risultato dato dall'input è uguale quello ottenuto da un certo numero "
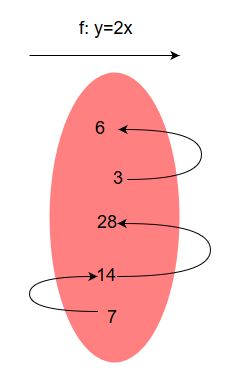
Poiché questa rappresentazione è più corretta, ma rischia di essere meno chiara, ci riserveremo la licenza di utilizzare una rappresentazione a due insiemi, ove questo aiuti nella comprensione.
FUNZIONI BIUNIVOCHE
La relazione vista nell'esempio precedente è chiaramente una funzione, in quanto per ogni numero esiste una sola immagine corrispondente al suo doppio. Poiché vale anche il contrario, cioè ogni output ha una sola controimmagine corrispondente (detto in altri termini: ogni ha una sola che è la sua metà), la funzione si definisce biunivoca. La biunivocità è molto importante perché una funzione può essere invertita solo se è biunivoca (affronteremo il concetto di funzione inversa nei prossimi capitoli).
Un altro modo per dire che una funzione è biunivoca è che non ci sono due input che generano output uguale. La relazione i delle iniziali vista prima è una funzione (perché ad ogni parola corrisponde una sola iniziale), ma non è una funzione biunivoca, perché non vale il viceversa (ad ogni iniziale corrispondono più parole).
NOTA LESSICALE: In termini rigorosi quando una funzione genera per ogni input un output differente non si dice biunivoca ma iniettiva.
Si definisce poi suriettiva una funzione per cui ogni elemento dell'insieme di destinazione è il risultato di qualche input (detto in altri termini più specifici: se ogni elemento dell'insieme di destinazione è controimmagine di un elemento dell'insieme di partenza, cioè se l'insieme di destinazione coincide con il codominio).
Utilizzando questa terminologia più avanzata, una funzione si dice biiettiva, o biunivoca, quando è sia iniettiva che suriettiva.
![La relazione nella figura è una [b]funzione[/b], perché ad ogni studente della classe 3A corrisponde una unica città di nascita. Però [b]non è iniettiva[/b] (ci sono più studenti che danno come "risultato" la stessa città di nascita) e [b]neppure suriettiva[/b] (esistono città dove non è nato nessuno di 3A). Quindi la funzione [b]non è biunivoca[/b].](https://beta.geogebra.org/resource/hcz5ffms/EdYcgPGRsLniC7MC/material-hcz5ffms.png)
Vediamo qui sotto alcuni esempi con una funzione matematica.
![La relazione matematica nella figura è una [b]funzione[/b], perché ogni numero ha un solo risultato se lo si eleva alla quarta. Però [b]non è iniettiva[/b] (un numero ed il suo opposto danno lo stesso risultato) e [b]neppure suriettiva[/b] (i numeri negativi non sono la quarta potenza di nessun numero). Quindi la funzione [b]non è biunivoca[/b].](https://beta.geogebra.org/resource/n4km4cdx/Ua1gt4VCUvkeKj8G/material-n4km4cdx.png)
La suriettività non è una condizione molto vincolante, perché se manca la si può ottenere lasciando invariata la legge della funzione e cambiando solo l'insieme di destinazione.
Nel nostro esempio se cambiamo l'insieme di destinazione della funzione da a , cioè prendiamo i risultati solo nell'insieme dei numeri positivi o nulli, tutti gli elementi dell'insieme di destinazione hanno una controimmagine nell'insieme di destinazione e la funzione è suriettiva.
![Se modifichiamo la funzione [math]\large{g}[/math], ed in particolare ridefiniamo il suo insieme di destinazione come i soli numeri reali positivi, cioè [math]\large{\mathbf{R_0^+}}[/math], la rendiamo [b]suriettiva[/b], perché [color=#ff0000]ogni elemento dell'insieme di destinazione[/color] è risultato di [almeno] [color=#3c78d8]un elemento dell'insieme di partenza[/color].
Continua però a [b]non [/b]essere [b]iniettiva[/b], quindi in definitiva [b]non è biunivoca[/b].](https://beta.geogebra.org/resource/pms92w38/URzzdY3yzZVs7mF6/material-pms92w38.png)
Per questo motivo possiamo dire che la condizione più importante per la biunivocità resta la prima, cioè l'iniettività, e quindi possiamo "confonderla" con essa e dire che se ogni input genera un risultato diverso (ogni risultato è risultato di un input differente) la funzione è biunivoca.
![In modo simile possiamo rendere [b]suriettiva[/b] la prima funzione che abbiamo visto considerando come insieme di destinazione quello composto dalle sole città dell'Italia continentale ed escludendo le isole.](https://beta.geogebra.org/resource/paykuxdh/oJmQshmvQtZHzhoP/material-paykuxdh.png)
Dato che la mancata suriettività può essere risolta in modo piuttosto semplice che non cambia la natura della funzione, possiamo dire che la condizione più importante per la biunivocità resta l'iniettività (cioè che due valori di input differenti non possano dare lo stesso risultato), e quindi possiamo "confonderla" con essa e dire che se ogni input genera un risultato diverso la funzione è biunivoca.