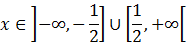Valor Absoluto (e inecuaciones)
1. Concepto
El valor absoluto de un número es el valor numérico del número (sin signo, que es lo mismo que con signo positivo).
El valor absoluto del número a se representa por |a|.
Ejemplos:
- |-1| = 1
- |-2| = 2
- |0| = 0
- |1| = 1
- |4,5| = 4,5
- |-0,3| = 0,3
- si el número es positivo, su valor absoluto es el propio número;
- si el número es negativo, su valor absoluto es su opuesto (número con signo opuesto, es decir, con signo positivo);
- si el número es 0, su valor absoluto es 0, aunque 0 no es ni positivo ni negativo.
2. Función Valor Absoluto
Matemáticamente, el valor absoluto es una función (de una variable) de los reales en los reales:
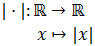
Podemos escribirla como una función a trozos:
Podemos escribirla como una función a trozos:
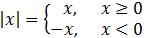
La función es continua en los reales y derivable en los reales excepto en 0.
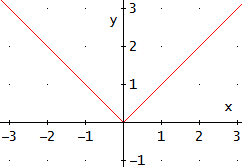
La gráfica de esta función es:
La función es continua en los reales y derivable en los reales excepto en 0.
La gráfica de esta función es:
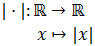
Podemos escribirla como una función a trozos:
Podemos escribirla como una función a trozos:
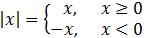
La función es continua en los reales y derivable en los reales excepto en 0.
La gráfica de esta función es:
La función es continua en los reales y derivable en los reales excepto en 0.
La gráfica de esta función es:

3. Propiedades
- El valor absoluto siempre es mayor o igual que 0, siendo 0 sólo cuando su argumento es 0:
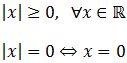
- El valor absoluto de un producto es el producto de los valores absolutos de los factores:
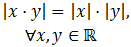
- Valor Absoluto de la suma:
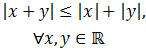
- Propiedad importante: si tenemos la desigualdad (menor o igual)
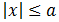 podemos escribir
podemos escribir
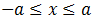 que es lo mismo que decir
que es lo mismo que decir
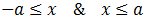 (tienen que cumplirse ambas relaciones).
Dicho en forma de intervalos:
(tienen que cumplirse ambas relaciones).
Dicho en forma de intervalos:
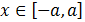 Si la desigualdad es (mayor o igual)
Si la desigualdad es (mayor o igual)
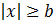 podemos escribir
podemos escribir
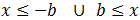 (es una unión: tiene que cumplirse una de las dos).
Dicho en forma de intervalos:
(es una unión: tiene que cumplirse una de las dos).
Dicho en forma de intervalos:
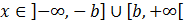
4. Ejemplos de Inecuaciones con Valor Absoluto
Vamos a resolver algunas inecuaciones con valor absoluto. Para ello usaremos la última propiedad del apartado anterior:
Ejemplo 1
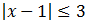 Podemos escribir la inecuación como
Podemos escribir la inecuación como
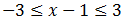
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:
Sumamos 1:
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:
Sumamos 1:
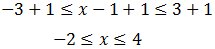
O bien, separar ambas inecuaciones y resolverlas por separado:
O bien, separar ambas inecuaciones y resolverlas por separado:
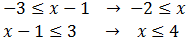 De ambas formas obtenemos la misma solución:
De ambas formas obtenemos la misma solución:
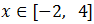 Ejemplo 2
Ejemplo 2
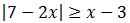 Debe cumplirse alguna de los dos inecuaciones:
Debe cumplirse alguna de los dos inecuaciones:
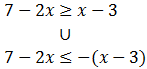
Resolvemos la primera:
Resolvemos la primera:
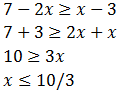 Resolvemos la segunda:
Resolvemos la segunda:
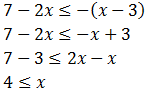 Por tanto, la solución es:
Por tanto, la solución es:
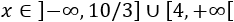
Ejemplo 3
Ejemplo 3
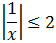
Tenemos las dos inecuaciones:
Tenemos las dos inecuaciones:
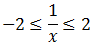
Resolvemos la primera:
Resolvemos la primera:
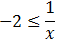
No podemos multiplicar por x porque no sabemos si es positiva o negativa.Supongamos que x es positiva ( x > 0): ahora sí podemos multiplicar por x :
No podemos multiplicar por x porque no sabemos si es positiva o negativa.Supongamos que x es positiva ( x > 0): ahora sí podemos multiplicar por x :
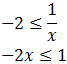
Por tanto, cambiando la desigualdad al dividir por el negativo -2, tenemos
Por tanto, cambiando la desigualdad al dividir por el negativo -2, tenemos
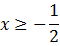
Pero hemos dicho que x > 0, luego al unir ambas condiciones tenemos que
Pero hemos dicho que x > 0, luego al unir ambas condiciones tenemos que

(ya que es la más restrictiva).Supongamos ahora que x es negativa: x < 0:
(ya que es la más restrictiva).Supongamos ahora que x es negativa: x < 0:
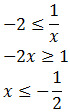
Por tanto, la solución a esta primera inecuación es
Por tanto, la solución a esta primera inecuación es
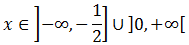
Resolvemos la segunda inecuación procediendo del mismo modo:
Resolvemos la segunda inecuación procediendo del mismo modo:
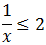
Si x es positiva:
Si x es positiva:
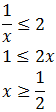
Si x es negativa:
Si x es negativa:
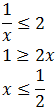
Por tanto, la solución a la segunda inecuación es:
Por tanto, la solución a la segunda inecuación es:
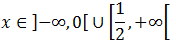
Las soluciones de las dos inecuaciones son:
Las soluciones de las dos inecuaciones son:
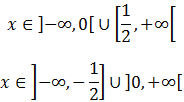
Y tienen que cumplirse ambas.
Por tanto, la solución es
Y tienen que cumplirse ambas.
Por tanto, la solución es
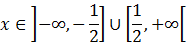
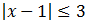 Podemos escribir la inecuación como
Podemos escribir la inecuación como
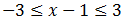
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:
Sumamos 1:
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:
Sumamos 1:
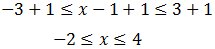
O bien, separar ambas inecuaciones y resolverlas por separado:
O bien, separar ambas inecuaciones y resolverlas por separado:
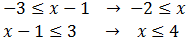 De ambas formas obtenemos la misma solución:
De ambas formas obtenemos la misma solución:
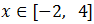 Ejemplo 2
Ejemplo 2
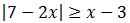 Debe cumplirse alguna de los dos inecuaciones:
Debe cumplirse alguna de los dos inecuaciones:
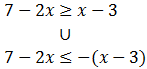
Resolvemos la primera:
Resolvemos la primera:
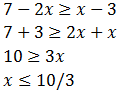 Resolvemos la segunda:
Resolvemos la segunda:
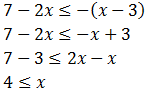 Por tanto, la solución es:
Por tanto, la solución es:
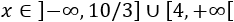
Ejemplo 3
Ejemplo 3
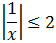
Tenemos las dos inecuaciones:
Tenemos las dos inecuaciones:
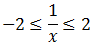
Resolvemos la primera:
Resolvemos la primera:
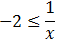
No podemos multiplicar por x porque no sabemos si es positiva o negativa.Supongamos que x es positiva ( x > 0): ahora sí podemos multiplicar por x :
No podemos multiplicar por x porque no sabemos si es positiva o negativa.Supongamos que x es positiva ( x > 0): ahora sí podemos multiplicar por x :
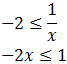
Por tanto, cambiando la desigualdad al dividir por el negativo -2, tenemos
Por tanto, cambiando la desigualdad al dividir por el negativo -2, tenemos
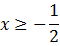
Pero hemos dicho que x > 0, luego al unir ambas condiciones tenemos que
Pero hemos dicho que x > 0, luego al unir ambas condiciones tenemos que

(ya que es la más restrictiva).Supongamos ahora que x es negativa: x < 0:
(ya que es la más restrictiva).Supongamos ahora que x es negativa: x < 0:
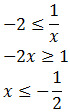
Por tanto, la solución a esta primera inecuación es
Por tanto, la solución a esta primera inecuación es
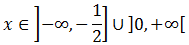
Resolvemos la segunda inecuación procediendo del mismo modo:
Resolvemos la segunda inecuación procediendo del mismo modo:
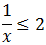
Si x es positiva:
Si x es positiva:
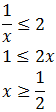
Si x es negativa:
Si x es negativa:
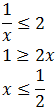
Por tanto, la solución a la segunda inecuación es:
Por tanto, la solución a la segunda inecuación es:
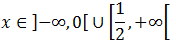
Las soluciones de las dos inecuaciones son:
Las soluciones de las dos inecuaciones son:
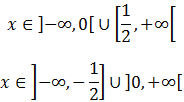
Y tienen que cumplirse ambas.
Por tanto, la solución es
Y tienen que cumplirse ambas.
Por tanto, la solución es