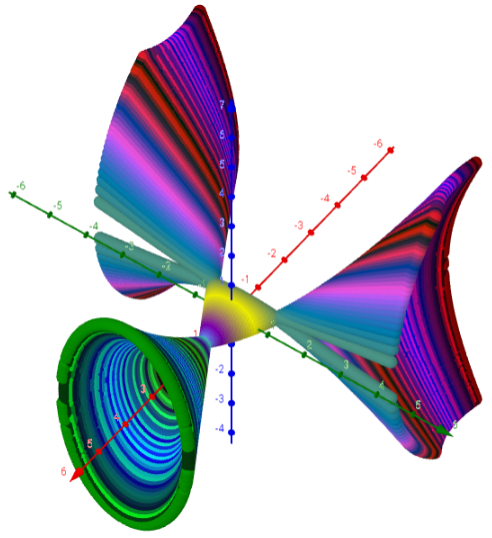
Bilder Oberflächen: implizite
x^4 = y^2 + z^2 (120x120 Punkte)
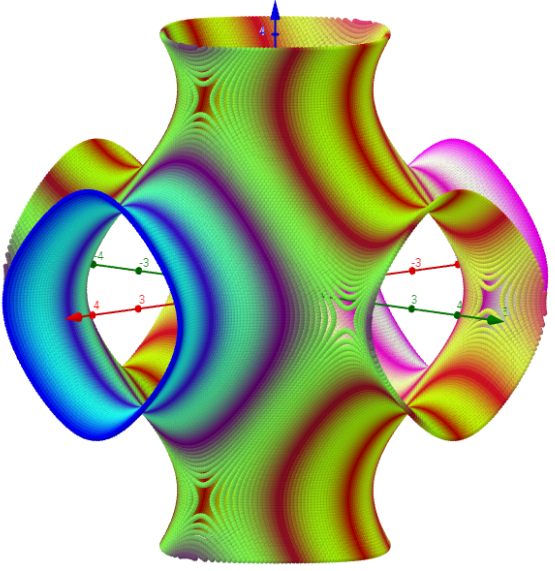
Amphora: cos(x)+cos(y)+cos(z)=0 (180x180 Punkte)
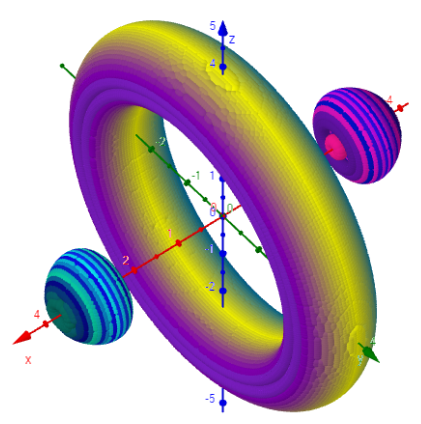
Elementarzelle: cos(x² / 2.2) + cos(y² / 2.2) + cos(z² / 2.2)=0 (90x90 Punkte)

Die Masken im Regal: x y sin(2z) + y z sin(2x) + z x sin(2y) =0.25 (80x80 Punkten)

Gumdrop Torus: 4 (x⁴ + (y² + z²)²) + 17x² (y² + z²)=0 (150x150 Punkte)
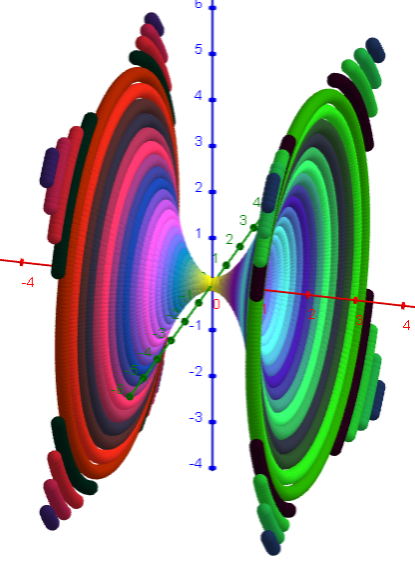
Kiss: x² + y² = (1 - z) z⁴ (150x150 Punkte)
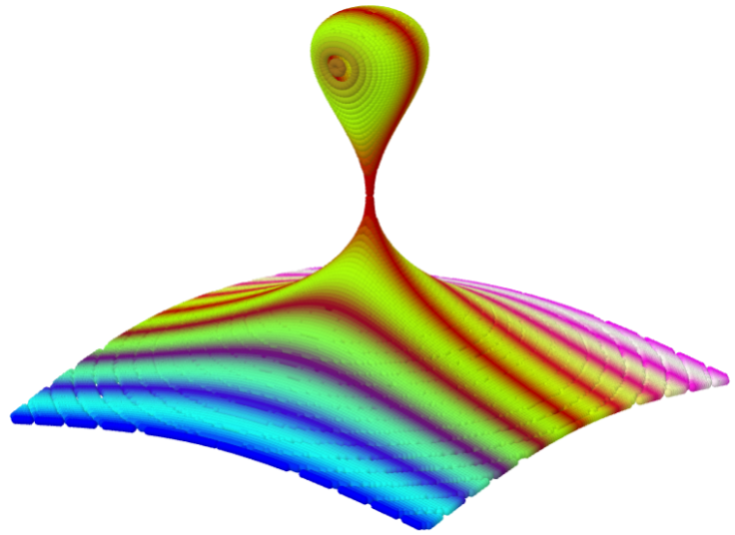
Horned Cube: -3x⁸ - 3y⁸ - 2z⁸ + 5(x² y z)² + 3(x y² z)² + 1 (150x150 Punkte)
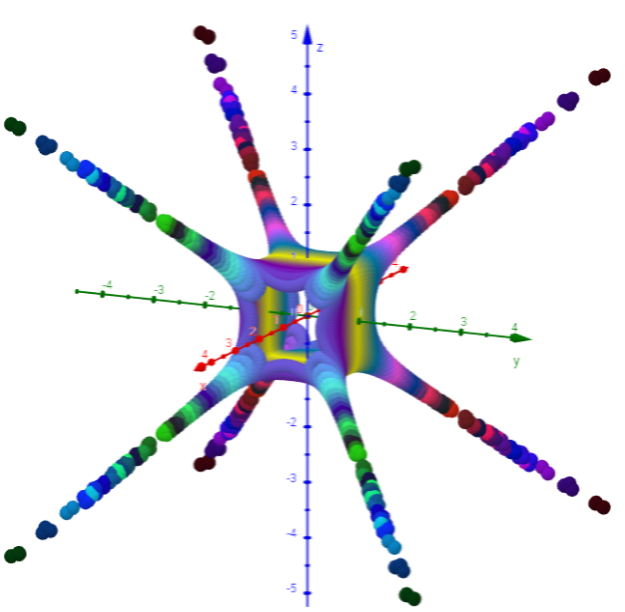
Hyperboloid: x^2+y^2=z^2 (120x120 Punkte)
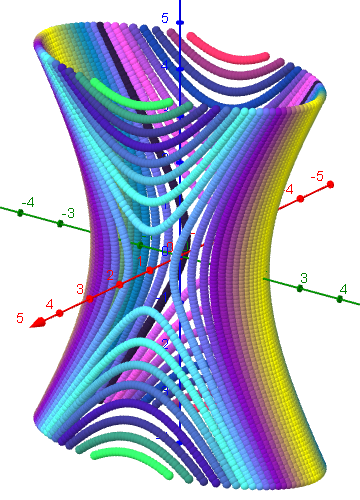
Atomic orbitals: cos((x y z) / 8) + 4cos((x² + y² + z²) / 4) = 3.35 (80x80 Punkte)

Tritrumpet: 8z² + (2x + 1) (3y² - (x - 1)²) (150x150 Punkte)