Uitleg + opgaven 19 en 20
Bekijk de grafiek van een startende zeilwagen. Je mag aannemen dat de snelheid constant toeneemt. De afgelegde afstand neemt dan kwadratisch toe. Voor de afgelegde afstand s (in meters) van de zeilwagen geldt s(t) =1,2⋅t2, waarin t de tijd in seconden is.
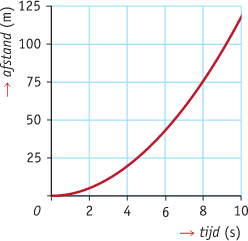
De gemiddelde snelheid over de eerste vier seconden bereken je met het differentiequotiënt:
\frac{\bigtriangleup s}{\bigtriangleup t}=\frac{1,2\cdot4^2-1,2\cdot0^2}{4-0}=\frac{19,2}{4}=4,8.
Die gemiddelde snelheid is dus 4,8 m/s.
Omdat de zeilwagen versnelt, is de snelheid op t = 4 hoger dan de gemiddelde snelheid over de eerste 4 seconden. Die snelheid op t = 4 kun je benaderen. Daarbij bereken je differentiequotiënten op steeds kleinere intervallen met t = 4 als beginwaarde.
Op het interval [4;4,1] is het differentiequotiënt:
Dit is een eerste benadering van de snelheid op t = 4.
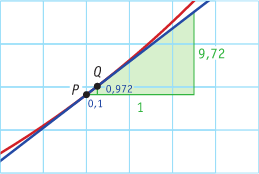
Bekijk de applet.
Schuif het blauwe punt (∆t).
Op het interval [4;4,01] is het differentiequotiënt:
Dit is een tweede en betere benadering van de snelheid op t = 4.
Je kunt de intervallen steeds kleiner maken en het differentiequotiënt uitrekenen.
Het lijkt er op dat het differentiequotiënt steeds dichter in de buurt van 9,6 uitkomt, naarmate de rechter grens van het interval dichter bij 4 komt.
| interval | differentiequotiënt |
| [4;4,1] | 9,72 |
| [4;4,01] | 9,612 |
| [4;4,001] | 9,6012 |
| [4;4,0001] | 9,60012 |
De snelheid op t = 4 kun je vinden door een rij van differentiequotiënten te berekenen op intervallen met als linker grens 4 en als rechter grens 4+∆t.
Die rij van differentiequotiënten benadert een bepaald getal naarmate de rechter grens dichter bij de linker grens komt, dus ∆t naar 0 gaat.
Dit getal is de snelheid op t = 4. Het lijnstuk PQ waarvan de richtingscoëfficient zo'n differentiequotiënt is, gaat over in een raaklijn aan de grafiek. Je noemt de gevonden waarde het differentiaalquotiënt op dat tijdstip.
Dit differentiaalquotiënt is de richtingscoëfficiënt van de raaklijn aan de grafiek van de functie in dat punt.
Opgave 19
Voor een versnellende zeilwagen geldt s = 1,8t2 waarin s de afgelegde afstand in meter en t de tijd in seconden is. Bekijk eerst bij de uitleg hoe de snelheid van een andere zeilwagen op een bepaald tijdstip wordt gevonden met behulp van een rij van differentiequotiënten.
a. De snelheid op t = 3 is:
c. Hoe groot is de snelheid op t = 3?
d. Hoe is de snelheid op t = 3 zichtbaar in de grafiek?
- hetzelfde als de gemiddelde snelheid over de eerste drie seconden.
- groter dan de gemiddelde snelheid over de eerste drie seconden.
- kleiner dan de gemiddelde snelheid over de eerste drie seconden.
| interval | differentiequotiënt |
| [3;3,1] | |
| [3;3,01] | |
| [3;3,001] | |
| [3;3,0001] |
- Als richtingscoëfficiënt van het lijnstuk op het interval [0,3].
- Als richtingscoëfficiënt van het lijnstuk op het interval [3;3,0001].
- Als richtingscoëfficiënt van de raaklijn aan de grafiek in het punt met t = 3.
- Als uitkomst bij t = 3.
Opgave 20
Voor de afgelegde afstand s (in meters) van een vallend voorwerp geldt de formule s = 4,9t2, waarbij t de tijd is in seconden. Na vijf seconden komt het voorwerp op de grond terecht.
a. Bepaal met behulp van kleine intervallen de snelheid van het voorwerp op t = 2.
b. Bepaal met behulp van kleine intervallen met welke snelheid het voorwerp op de grond terechtkomt.