Esquema
Teorema de Mamikon
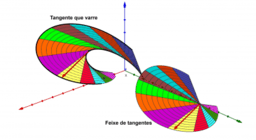
O Teorema de Mamikon traz um método intuitivo e dinâmico para o cálculo de áreas. Utilizando-se deste método podemos determinar diversas áreas, dadas antes por Integrais, requerendo agora um conhecimento mais modesto da Matemática Elementar. Podemos citar alguns exemplos como a área sob algumas funções elementares em R2, os problemas de área da Cicloide e Trocoide, superfícies geradas a partir de curvas suaves em R3, entre outros.
Esta apresentação mostra uma pequena parte da evolução do Teorema de Mamikon, algumas aplicações à funções em R2 e um modelo customizável de superfícies em R3. Tem também como objetivo auxiliar a compreensão dos leitores do artigo Uma apresentação do Teorema de Mamikonda da Revista RECEN de __ / 2017.
Não temos a intenção de trazer demonstrações ou explicações formais nesta apresentação devido à limitação de espaço.
Para mais informações e compreensão do Teorema de Mamikon sugerimos consultar:
Dissertação de Mestrado da UFABC disponível no site do Profmat ou diretamente no link https://sca.profmat-sbm.org.br/sca_v2/get_tcc3.php?id=95652
Artigo da Revista RECEN disponível em http://revistas.unicentro.br/index.php/RECEN/issue/viewIssue/290/pdf_5
O trabalho original de Mamikon Mnatsakanian e Tom Apostol é apresentado no livro New Horizons in Geometry, ISBN 978-0883853542, 2012.