Theorie
Bekijk de applet: Differentiaalquotiënt.
Je ziet een deel van de grafiek van de functie y = f(x).
Sleep het blauwe punt ∆x.
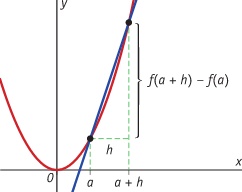
De gemiddelde verandering van de functie f op het interval [a,b] is:
De verandering in een punt met x = a van de functie f vind je door het differentiequotiënt op [a,a+h] te berekenen, waarbij je h steeds dichter bij 0 kiest:.
Voor x = a krijg je dan een rij met differentiequotiënten. Deze rij benadert een bepaald getal. Dit getal heet het differentiaalquotiënt voor x = a.
In plaats van voor x = a, schrijf je ook wel
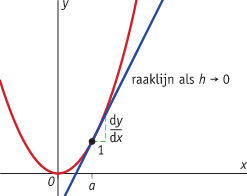
In de grafiek is het differentiaalquotiënt gelijk aan:
- de richtingscoëfficiënt van de raaklijn in het punt van de grafiek met x = a
- de helling van de grafiek in het punt x = a
- de snelheid waarmee y verandert voor x = a