lint rond een doos
Je moet een doos inpakken met een lint van 2m lang. De afmetingen van de doos mag je zelf kiezen.
Bepaal de afmetingen om een zo groot mogelijke doos te kunnen inpakken.
 rekenvoorbeeld
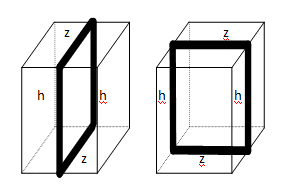
om het lint rond de doos te binden, heb je in het totaal 4 keer de hoogte nodig en 4 keer de zijde van het grondvlak.
We vinden: 4z + 4h = 200.
Als we als zijde 10 cm nemen: 200 - 4 . 10 = 160
4h = 160
h = 40
De inhoud van de doos wordt: 10 . 10 . 40 = 4 000cm³
Als we als zijde 20 cm nemen: 200 - 4 . 20 = 120
4h = 120
h = 30
De inhoud van de doos wordt: 20 . 20 . 30 = 12 000cm³
van rekenvoorbeeld naar onbekende x:
Als we als zijde 20 cm nemen, krijgen we: 200 - 4x = 4h
50 - x = h.
De inhoud van de doos wordt x . x. (50 - h)
berekenen:
I (x) = x . x . (50 - x)
I (x) = - x³ + 50x²
I ' (x) = - 3x² + 100x
Om de maximale waarde van de inhoud te vinden moet de afgeleide gelijk worden aan 0.
We vinden:
- 3x² + 100x = 0
x . ( -3x + 100) = 0
Oplossingen zijn x = 0 en x = 100/3 = 33,3
In een tekenoverzicht:
x 0 33,3
I ' (x) = -3x? + 100 - 0 + 0 -
I (x) ↘ min ↗ max ↘
Het zinvol domein = [ 0 , 50 ]
want met een zijde van 50cm is het lint van 2m al op aan de zijden alleen al.
Als oplossing vinden we:
De zijde van de doos = x = 33,3 cm
De hoogte van de doos = 50 - x = 16,7 cm
controle:
de totale lengte die we gebruiken bij het inpakken is 4 . 33,3 + 4 . 16,7 = 200.
Ga nu in het applet na of de gevonden waarden inderdaad een maximale inhoud opleveren.
rekenvoorbeeld
om het lint rond de doos te binden, heb je in het totaal 4 keer de hoogte nodig en 4 keer de zijde van het grondvlak.
We vinden: 4z + 4h = 200.
Als we als zijde 10 cm nemen: 200 - 4 . 10 = 160
4h = 160
h = 40
De inhoud van de doos wordt: 10 . 10 . 40 = 4 000cm³
Als we als zijde 20 cm nemen: 200 - 4 . 20 = 120
4h = 120
h = 30
De inhoud van de doos wordt: 20 . 20 . 30 = 12 000cm³
van rekenvoorbeeld naar onbekende x:
Als we als zijde 20 cm nemen, krijgen we: 200 - 4x = 4h
50 - x = h.
De inhoud van de doos wordt x . x. (50 - h)
berekenen:
I (x) = x . x . (50 - x)
I (x) = - x³ + 50x²
I ' (x) = - 3x² + 100x
Om de maximale waarde van de inhoud te vinden moet de afgeleide gelijk worden aan 0.
We vinden:
- 3x² + 100x = 0
x . ( -3x + 100) = 0
Oplossingen zijn x = 0 en x = 100/3 = 33,3
In een tekenoverzicht:
x 0 33,3
I ' (x) = -3x? + 100 - 0 + 0 -
I (x) ↘ min ↗ max ↘
Het zinvol domein = [ 0 , 50 ]
want met een zijde van 50cm is het lint van 2m al op aan de zijden alleen al.
Als oplossing vinden we:
De zijde van de doos = x = 33,3 cm
De hoogte van de doos = 50 - x = 16,7 cm
controle:
de totale lengte die we gebruiken bij het inpakken is 4 . 33,3 + 4 . 16,7 = 200.
Ga nu in het applet na of de gevonden waarden inderdaad een maximale inhoud opleveren.