Right-angle-Hypotenuse-Side
RHS Illustrated
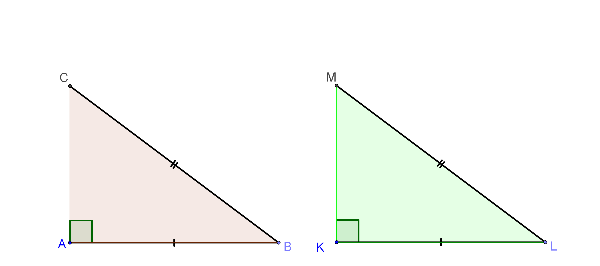
RHS Explained
If the hypotenuse and one side of a right-angled triangle are congruent to the corresponding parts of another right triangle, the right-angled triangles are congruent.
Remember during SSS we also experience that the triangle became a right-angle triangle when the sides were Pythagorean Triples. Read more about Pythagorean Triples by clicking here:
We can always use the Pythagorean Theorem to work out the third side and the use the SSS-Approach to construct this. But, this is a special case of ASS that will be discussed in more detail under the section about problematic methods. (See the "Donkey Theorem" for more details)
Below is an example how to construct this. If you change anything in the construction, just click on the arrows on the top right to restore the construction.
Example: Constructing RHS
Steps in Constructing RHS
Now you try to draw a triangle congruent to the previous one You need to draw a triangle with side AB=8cm, right angle CAB and hypotenuse of 10cm. Try to do this in the "Applet" below
- Use
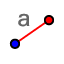 to draw segment AB and if you are requested to give the length type in 8
to draw segment AB and if you are requested to give the length type in 8 - Use
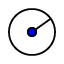 to draw a circle at point B and if requested to enter a radius type in 10
to draw a circle at point B and if requested to enter a radius type in 10
- Use
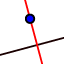 to draw a line perpendicular to line AB through point A. (Click on line AB and then point A.)
to draw a line perpendicular to line AB through point A. (Click on line AB and then point A.) - Use
 to place point C at the intersection of the perpendicular line and the circle
to place point C at the intersection of the perpendicular line and the circle - Use
 to draw triangle ABC
to draw triangle ABC