Attività 2 poligono circoscritto
Teorema
Se un poligono è:
- inscritto in una circonferenza, gli assi dei suoi lati si incontrano nel centro della circonferenza
- circoscritto a una circonferenza, le bisettrici dei suoi angoli si incontrano nel centro della circonferenza
- Disegniamo una circonferenza
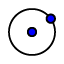
- Scegliamo su essa 5 (o più) punti a piacere
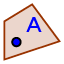
- Costruiamo la retta tangente alla circonferenza e passante per ciascuno dei punti
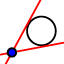[Attenzione per tracciare riga e compasso ricordiamo che la tangente è perpendicolare al raggio nel punto di contatto] - Troviamo i punti di intersezione di ciascuna coppia di tangenti (consecutive)
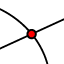
- Congiungiamo i punti così trovati
oppure utilizziamo il comando poligono 
Verifichiamo che il nostro poligono verifica la definizione di poligono circoscritto. - Costruiamo le bisettrici di ciascun angolo del poligono
Osserviamo
1) le bisettrici si incontrano tutte
2) Tale punto coincide con
Proviamo a spiegare perché.
1) Cosa è la bisettrice di un angolo?
2) Quali proprietà hanno i punti della bisettrice
3) Da ciascun vertice i due lati sono tangenti alla circonferenza e per il teorema a pag. G130 la bisettrice dell'angolo coincide con