El joc de la vida
Sabies que es poden usar models per simular organismes vius a l’ordinador?
En el camp de les biomatemàtiques, per exemple, s’usen aquests simuladors per entendre el comportament del virus de la sida o el d’Ebola. I en el món de la informàtica, aquests simuladors van originar l’emblema dels hackers…
Visió general
Per a programar el simulador ens basarem en un model fet famós pel matemàtic John Conway anomenat Joc de la Vida, mira el següent vídeo introductori:
El Tauler
Com has pogut veure, ens cal:
- un tauler quadriculat
- exemple d’un tauler de 3×3:
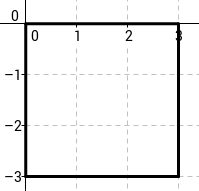
- on a cada cel·la del tauler (quadricula) hi pot habitar un individu o estar buida
- exemple d’un individu a la cel·la que està a la segona fila, tercera columna:
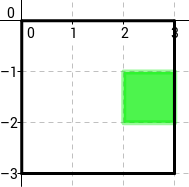
- en funció de les cel·les veïnes
- exemple on l’individu (de color verd) té dos veïns (blaus):
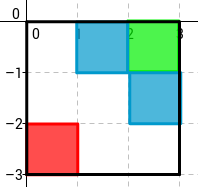
- fixa’t que són veïns aquells individus que comparteixen com a mínim un vèrtex.
Les Regles
També hauràs vist que el Joc de la Vida, no es tracta d’un joc amb diversos jugadors. Sinó que un cop estableixes els individus que hi ha inicialment (comunitat inicial), aquests van naixent o morint en funció de les següents regles (anomenades lleis genètiques):
- Llei de Mortalitat: només sobreviuen els individus amb 2 o 3 veïns.
- exemple on l’individu vermell morirà de solitud:
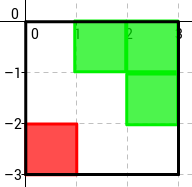
- exemple on l’individu vermell morirà per sobrepoblació:
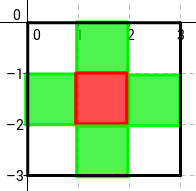
- Llei de Reproducció: neixen nous individus a les cel·les buides que tenen exactament 3 veïns.
- exemple on naixerà un individu a la segona fila, segona columna:
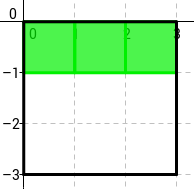
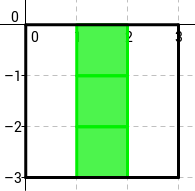
Pregunta Inicial: Quines morts i naixements hi hauria en el següent tauler? (dibuixa el següent estat del tauler i indica les coordenades (fila i columna) dels individus que moririen i naixerien)
L'aplicació programada en JavaScript dins de Geogebra
A continuació pots veure el joc ja programat en JavaScript dins de Geogebra. De forma que podràs fer proves i contestar a les preguntes que hi ha més avall.
(Si volguessis programar el joc tu mateix dins de Geogebra, fes una ullada a aquesta activitat d'EduLogix: GeoJS: Vida Artificial )
L'aplicació programada en JavaScript dins de Geogebra
A continuació pots veure el joc ja programat en JavaScript dins de Geogebra. De forma que podràs fer proves i contestar a les preguntes que hi ha més avall.
(Si volguessis programar el joc tu mateix dins de Geogebra, fes una ullada a aquesta activitat d'EduLogix: GeoJS: Vida Artificial )
Investiga
Ara que tens un laboratori de vida artificial, pots fer investigacions sobre l’evolució de diferents comunitats d’individus.
- Botó "New Cell": crea un nou individu que pots moure amb el ratolí a la casella desitjada (pots suprimir individus amb la tecla Suprimir o posant-los sobre un altre d'existent).
- Botó "Run 1 step": per aplicar les regles un cop i veure quins individus moren o neixen i per tant, com evoluciona la comunitat.
- Botó "Reset": per deixar el tauler en blanc.
- Pregunta 1: Què passa si proves una comunitat que només té un individu inicialment? Depèn de la posició al tauler?
- Pregunta 2: Què passa si la comunitat inicial és de dos veïns? Quantes possibilitats diferents hi ha? Depèn de la posició relativa entre individus? Depèn de la posició al tauler?
- Si tens un tauler gran, pots provar què passa a diferents comunitats si les poses separades entre si.
- Pregunta 3: Què passa si poses tres individus en diagonal? Passa el mateix amb qualsevol comunitat que estigui en diagonal?
- Repte 1: Investiga les comunitats amb tres individus.
- Fes proves amb totes les comunitats amb tres individus inicials que no estiguin separats. I observa si els passa alguna d’aquestes situacions:
- Extinció: la població desapareix.
- Estabilitat: la població resta igual.
- Oscil·lació: la població no creix ni decreix, simplement canvia de forma periòdicament.
- S’anomena polyplet (o polyking) a qualsevol conjunt de cel·les connectades ortogonalment o diagonalment. Exemple polyplets de tres components (o triplets):
- Fes proves amb totes les comunitats amb tres individus inicials que no estiguin separats. I observa si els passa alguna d’aquestes situacions:

- Pregunta 4: Quina evolució ha fet cadascun dels triplets? (si són oscil·ladors, indica el període)
- Repte 2: Investiga els tetrominos.
- Si en comptes d’haver 3 individus inicials, n’hi ha 4, el nombre de possibilitats augmenta a 22! Aquest cop doncs, enlloc d’investigar els polyplets de 4 (tetroplets), només n’investigarem un subconjunt d’aquests, els que no tenen individus en diagonal, que s’anomenen tetrominos: (Hi ha qui també els anomena tetriminos ja que són els que apareixen al joc d’ordinador Tetris)
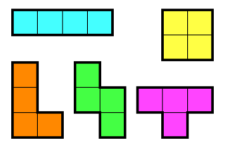
- Pregunta 5: Quina evolució ha fet cadascun dels tetrominos? (si són oscil·ladors, indica el període)
- Pregunta 6: Pots proposar un tetroplet (no inclòs en els tetrominos anteriors) i explicar com evoluciona?

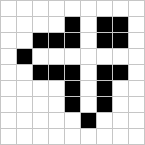
- Pregunta 10: Pots trobar algun altra població que també sigui depredadora?
- Pregunta de Síntesi 1: Et veuries capaç de descriure un parell de situacions on et podrien ser útils les tècniques que après en aquesta activitat?
- Pregunta de Síntesi 2: Quina relació veus entre les formes complexes de la bandada d’ocells del següent vídeo i l’activitat que acabes de fer?