Theorie
Hellingsgrafiek
Bekijk de applet.
Een functie y = f(x) heeft meestal in een punt van de grafiek een helling die wordt bepaald door het differentiaalquotiënt in dat punt.
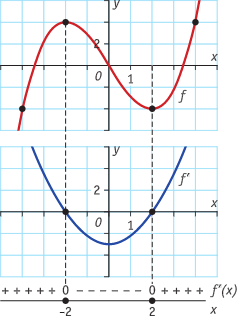
Van die hellingsgetallen kun je ook weer een grafiek maken. Je ziet de grafiek van een functie (in rood) met de hellingsgrafiek (in blauw). De bijbehorende functie van de hellingsgrafiek wordt de hellingsfunctie of afgeleide van f genoemd en kun je korter schrijf als f' (spreek uit f accent). Je ziet:
- als de hellingsfunctie positieve waarden heeft, stijgt de bijbehorende functie;
- als de hellingsfunctie negatieve waarden heeft, daalt de bijbehorende functie;
- met wat voor soort stijging/daling je te maken hebt;
- waar de hellingsfunctie de waarde 0 heeft, heeft de grafiek van de bijbehorende functie een horizontale raaklijn; vaak gaat het daarbij om extremen van de functie.