Golf
You are building a new golf facility. You want to construct a driving range. In this driving range is a two-story building that golfers practice driving out of, as seen in the picture below.

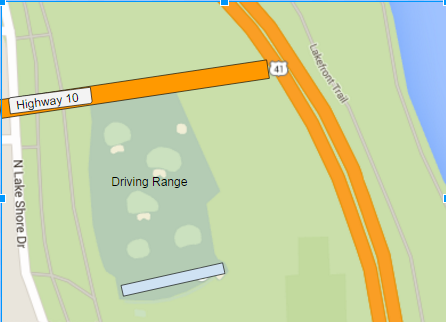
On the block next to the driving range is a well-traveled road (Highway 10), as seen in the picture below. The distance from the road to the building is 250 feet.
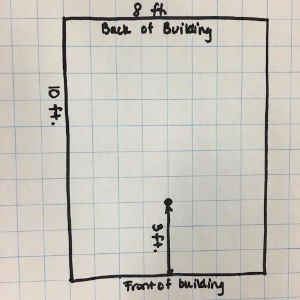
Each story of this building is 11 feet tall. From the front of the building to the back of the building is 10 feet. The roof of the top level sticks out 5 feet farther than the floor. You tee-off three feet from the front of the building, which is shown below.
You need to put a net up where the driving range meets the road, to ensure that no cars are damaged by golf balls. In order for the city to approve the building of the driving range, they need to be convinced that the net will not allow golf balls over it. Your job is to apply your knowledge of quadratic functions to determine how high the net needs to be to ensure that no cars are damaged by flying golf balls and to present a convincing argument to the city that will prove the net is high enough to protect against traffic incidents.