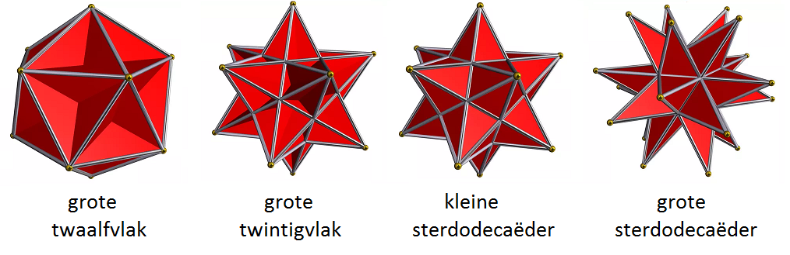
Kepler-Poinsot lichamen
Bij het bestuderen van de platonische lichamen zagen we al dat je een regelmatig twintigvlak (icosaëder) kan bekijken als het in elkaar schuiven van 12 piramides met vijfhoekig grondvlak.
De Franse wiskundige Louis Poinsot stelde zich in 1810 de vraag: "Wat bekom ik als ik van deze piramides enkel de grondvlakken overhoud?".
Poinsot ontdekte een nieuw regelmatig veelvlak, opgebouwd uit 12 regelmatige vijfhoeken. Hij noemde het lichaam "Le Grand dodécaèdre" (het grote twaalfvlak). Had Poinsot een zesde platonisch lichaam ontdekt? Het nieuwe lichaam bestaat inderdaad uit congruente regelmatige veelvlakken en ook de hoekpunten zijn congruent. Maar... het lichaam is niet convex, d.w.z. de twaalf vijfhoeken snijden elkaar.
In volgend applet zie je de 12 vijfhoeken van het grote twaalfvlak verschillend ingekleurd.
Maar hoeveel van deze niet-convexe regelmatige veelvlakken kan je maken?
Poinsot ontdekte dat hij een analoog lichaam kon opbouwen vanuit een regelmatig twintigvlak. Johannes Kepler beschreef reeds in 1619 twee stervormige lichamen. En in 1813 bewees Cauchy dat met deze vier lichamen het rijtje volledig was. Met zijn vier vormen ze, naar hun ontdekkers, de Kepler-Poinsot lichamen.