Perpendicular Besectors
Understand the Meaning of a Perpendicular Bisector.
Step 1.With the circle tool center at point at A, draw arcs or circles with the same radius above and below AB.The arcs should have a radius greater than 1/2 the length of AB.
Step 2. Using the same radius, place the compass point at B and draw arcs above and below. Label the points where the arcs intersect as E and F.
Step 3. Use a straightedge to draw a line through E and F.
Construct the perpendicular bisector of a given line segment.
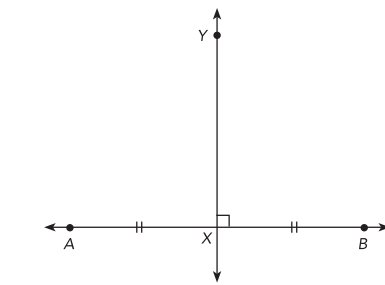
Bisect line segment AB.
Guided Practice
Draw the perpendicular bisector of line segment XY.
Apply perpendicular bisectors in real-world problems.
Officials want to build a water purification plant that will be used by three towns. The water purification plant must be equidistant from all three towns. Describe how you find the location of the purification plant.
Apply perpendicular bisectors in real-world problems.
Officials want to build a water purification plant that will be used by three towns. The water purification plant must be equidistant from all three towns. Describe how you find the location of the purification plant.
Draw each line segment and construct its perpendicular bisector.
XY = 5cm
Draw each line segment and construct its perpendicular bisector.
PQ = 6.8 cm
Draw each line segment and construct its perpendicular bisector.
MN = 11 cm
Draw a line segment between 4 inches and 5 inches and label the endpoints M
and N. Construct the perpendicular bisector of MN.
Explain briefly if you could construct a different perpendicular bisector of MN
Draw the perpendicular bisectors of PQ and PR. Label the point where the two perpendicular bisectors meet as W.
Draw the perpendicular bisectors of PQ and PR. Label the point where the two perpendicular bisectors meet as W.