combine by dragging
controlled dragging
There are Exercise Tools that are conceived for this kind of exercises while GeoGebra isn't. But with some magic and an advanced skill level you can do this in GeoGebra to. The reward of it is very nice as you can see in next applet
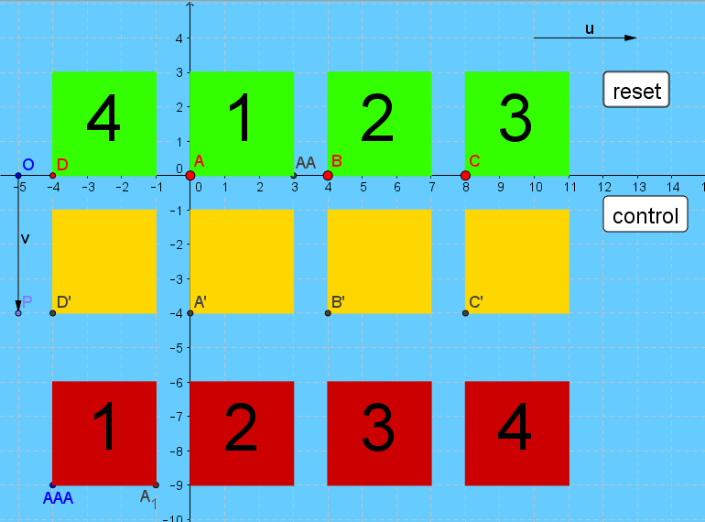
See how it works: Goal is to drag the red squares to the yellow squares under the corresponding green ones. Instead of 1, 2, 3 and 4 you can of course insert equations, graphs, sign or slope tables.
- The control button puts the wrong placed squares back to their initial position
- The reset button puts all back to its initial position.
How the magic works
construction
- Type the command list1 = Shuffle[{(-4, 0), (0, 0), (4, 0), (8, 0)}] to define list1.
- Define the points A = list1(1), B = list1(2), C = list1(3) and D = list1(4). These points are the the lower left corners of the green squares at a randomized position
- Define AA = A + u, BB = B + u etc. to define the lower right corners of the green squares.
- Create the 4 green squares as Polygon[A, AA, 4] etc.
- Create the 4 yellow squares as a vertical translation e.g. Translate[polygon1, v]. The translations of the lower left corners willl be named as A', B', C' and D'.
- Create the 1st red square starting from a point AAA and A1 = AAA + u as Polygon[AAA, A1, 4]. Create in a similar way the other red squares.
- Link the position of graphs, equations, texts... to the points A, B, C and D and the corresponding points AAA, BBB, CCC and DDD. Open the properties and mark them as selection not allowed. Now you can drag the red squares and the linked objects will follow the dragging.
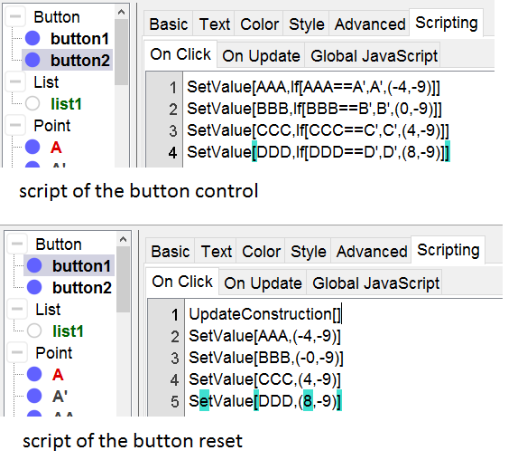
- create a button with caption control. It will control the combinations by evaluating the positions of the lower left corners of the red squares: AAA has to be equal to A' etc.
- If AAA = A' the combination is correct. If not AAA will be set back to its initial position.
- The script of this button resets the red squares back to their initial position.
- UpdateConstruction[] reshuffles list 1 and thereby the position of A, B, C and D.
scripts of the two buttons
Don't start with this kind of applets if your a GeoGebra starter.
But if you are a skilled user, it's a challenge with a nice reward!
I used this kind of exercise to combine the graphs of functions and their derivates on hellingsgrafieken.