L'asse di un segmento come luogo geometrico
L'asse di un segmento è quella retta perpendicolare ad esso che passa per il suo punto medio.
Tutti i punti dell'asse condividono una proprietà, costituiscono quindi un luogo geometrico.
Un luogo geometrico è un insieme di punti che hanno una stessa proprietà in comune. L'esempio più semplice di luogo geometrico è la circonferenza: la proprietà che hanno in comune i suoi punti è che hanno tutti la stessa distanza da un determinato punto, detto "centro" della circonferenza (mentre la misura di tale distanza è chiamata "raggio").
![I punti [math]\textcolor{#007700}{P_1}[/math], [math]\textcolor{#007700}{P_2}[/math], [math]\textcolor{#007700}{P_3}[/math] e [math]\textcolor{#007700}{P_4}[/math], come tutti i punti sulla circonferenza in figura, [b]hanno una proprietà in comune: la loro distanza dal punto [/b][b][math]\textcolor{red}{C}[/math] è sempre la stessa[/b]. La circonferenza quindi è un [b]luogo geometrico[/b].](https://beta.geogebra.org/resource/ygs5dd4t/HdyZGjB0wXqp9ykW/material-ygs5dd4t.png)
La proprietà che hanno in comune i punti dell'asse di un segmento è che sono tutti equidistanti dai due estremi del segmento (cioè la loro distanza da uno degli estremi è sempre uguale alla distanza dall'altro). Chiariamo il concetto nell'animazione qui sotto.
La retta rossa è l'asse del segmento AB. e sono due punti dell'asse, e puoi vedere che per entrambi la distanza da è congruente alla distanza da .
Puoi anche trascinare il punto P lungo l'asse e vedere che le due distanze da e da restano identiche.
Vediamo la dimostrazione di questa proprietà, attraverso un teorema.
Fai attenzione a due aspetti importanti:
- se segni sul disegno tutte le informazioni di cui sei in possesso (ad esempio marchi con lo stesso simbolo due elementi congruenti) è più facile che tu riesca a sfruttarle per i tuoi ragionamenti.
- parti da quello che conosci: dato che conosciamo solo i criteri di congruenza dei triangoli, molto spesso le nostre dimostrazioni passeranno attraverso il confronto di triangoli. Quindi cerca nel tuo disegno i triangoli che ti sembrano congruenti... ;)
VALE IL TEOREMA INVERSO?
Abbiamo dimostrato che SE un punto appartiene all'asse di un segmento ALLORA è equidistante dai due estremi.
Vale anche l'implicazione opposta?
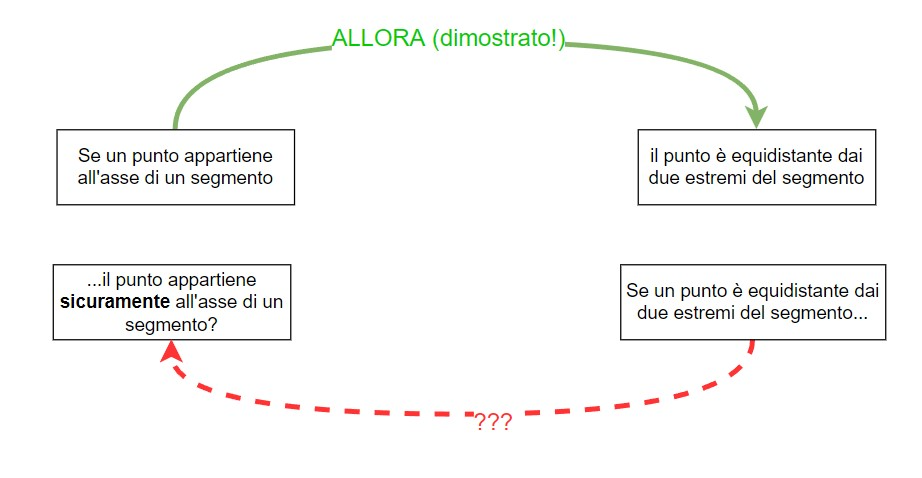
Ricordiamo che una implicazione SE... ALLORA NON implica necessariamente anche la sua inversa sia valida, come mostra questo semplice esempio.
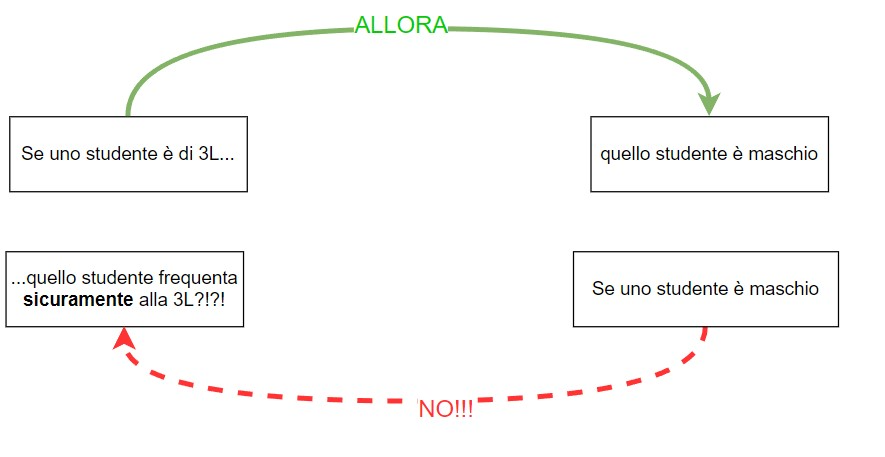
(puoi ripassare il concetto di implicazione in modo più dettagliato nel paragrafo contenuto dopo la dimostrazione di questa pagina)
Possiamo dire di sì. Infatti:
- se allora unendo C ad A ed a B otteniamo un triangolo isoscele
- se ABC è isoscele, la altezza, la mediana e la bisettrice relative alla base coincidono (lo abbiamo dimostrato nei corollari sulle proprietà dei triangoli isosceli, che trovi in questa pagina).
- Quindi se disegniamo l'altezza CH che passa per C essa è anche mediana, e di conseguenza è l'asse di AB (è perpendicolare ad AB perchè altezza e passa per il punto medio perché è mediana),
- quindi C appartiene all'asse di AB. C.V.D.
Se nella costruzione invece di tracciare la retta che passa per il punto medio fossimo partiti dall'altra caratteristica dell'asse, cioè che è perpendicolare al segmento, saremmo riusciti a dimostrare che i due triangoli così ottenuti erano congruenti? Perché?
Fai il disegno e prova a rispondere.