Verhalten im Unendlichen
Wir wissen von ganzrationalen Funktionen bereits, dass für der Summand mit dem höchsten Exponenten das Verhalten dominiert und es daher genügt, ihn allein zu betrachten.
Wem das nicht mehr klar ist, der kann hier klicken, um es zu wiederholen.
Dasselbe Prinzip machen wir uns auch bei gebrochen-rationalen Funktionen zunutze, wenden es dabei aber auf Zähler und Nenner getrennt an. Dabei können grundsätzlich drei verschiedene Fälle vorkommen:
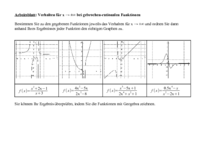
1. Fall: Zählergrad > Nennergrad
Beispiel: ; , denn im Zähler und Nenner
dominieren jeweils die Summanden mit dem höchsten Exponenten das Verhalten im Unendlichen.
(im vorletzten Schritt wurde gekürzt)
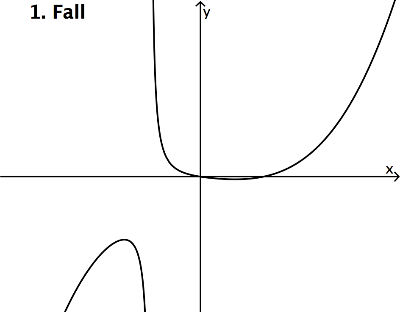
2. Fall: Zählergrad = Nennergrad
Beispiel: ;
D.h. im Unendlichen (ganz links bzw. ganz rechts) nähert sich der Graph dem Wert y = -1/2. Der Graph hat also
eine waagerechte Asymptote. Waagerechte Asymptoten kommen bei ganzrationalen Funktionen nicht vor, sind also
etwas Neues.
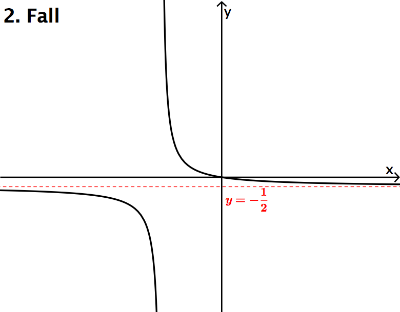
3. Fall: Zählergrad < Nennergrad
Beispiel: ;
D.h. im Unendlichen (ganz links bzw. ganz rechts) nähert sich der Graph der x-Achse (y = 0), die damit eine
waagerechte Asymptote ist. Das lässt erkennen, dass der Graph sich rechts von oben und links von unten der x-
Achse nähert.
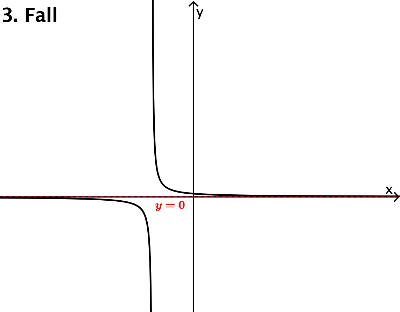
Sie können nun überprüfen, ob Sie es verstanden haben, indem Sie folgendes Aufgabenblatt bearbeiten.