La chambre obscure: machine à multiplier
Les outils de dessin de la renaissance, comme illustrés dans la gravure suivante d'Albrecht Dürer sont des machines à multiplier, en général par un facteur plus petit que un, c'est-à-dire à réduire un modèle réel de grande taille en un dessin qui tient sur une page.
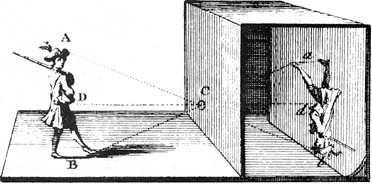
La chambre obscure est un outil à dessiner en perspective, une autre machine à multiplier, par un nombre négatif cette fois-ci.
La multiplication n'opère donc pas seulement sur les nombres, mais sur les points de la droite et les points du plan (qui sont aussi des nombres). Cette opération de multiplication, c'est l'agrandissement et la réduction. Comme les points sont sans dimension, l'agrandissement n'agit pas sur eux de manière spectaculaire. Voyons le plutôt sur une image du plan.
La chambre obscure est un outil à dessiner en perspective, une autre machine à multiplier, par un nombre négatif cette fois-ci.
La multiplication n'opère donc pas seulement sur les nombres, mais sur les points de la droite et les points du plan (qui sont aussi des nombres). Cette opération de multiplication, c'est l'agrandissement et la réduction. Comme les points sont sans dimension, l'agrandissement n'agit pas sur eux de manière spectaculaire. Voyons le plutôt sur une image du plan.Bougez le modèle et le plan de projection. Ils peuvent être placés soit en position "Dürer", c'est-à-dire où la convergence des droites, l'objectif, se trouve être l'œil de l'artiste, avec le plan de projection entre le modèle et l'objectif, soit en position "chambre obscure" (déjà connue d'Aristote!), où l'objectif est un trou dans la chambre noire, le plan de projection étant par delà cet objectif. Dans le premier cas, le rapport des longueurs algébriques est positif, dans le deuxième, il est négatif.
Cochez la case "Réquerres" pour voir apparaitre une réquerre, mesurant les nombres positifs au dessus de l'horizon, négatifs en dessous. Quand c'est cette image qu'on agrandit ou réduit, cette machine devient une machine à multiplier. Rapprochez la réquerre à l'échelle 1 de la réquerre multipliée. Localisez le 1 de la réquerre transformée, "zoomez", et remarquez qu'il est aligné avec le rapport de l'autre (si le rapport d'agrandissement est de -0.56 par exemple, +1 est aligné avec -0.56 sur celle à l'échelle 1/1). Si vous vous demandez combien font -1.2 * -0.56, localisez -1.2 et lisez en face, sur la règle à l'échelle 1, le résultat.