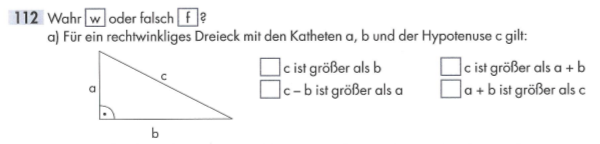
Die Dreiecksungleichung und die Ellipse
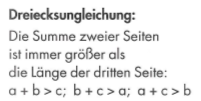
Die Dreiecksungleichung
Da Ungleichungen in diesem Bereich von GeoGebra nicht unterstützt sind, muß eine Gleichung benutzt werden:
Ortsliniengleichung[a+b==c, C]:GeoGebra liefert aber eine Gerade, nicht nur eine Strecke. Im Hintergrund steht, dass die Gleichung a+b=c in GeoGebra (aus mathematischen Gründen) immer als (a+b=c) oder (b+c=a) oder (c+a=b) interpretiert wird.
Verallgemeinerung: die Definition einer Ellipse

Der Befehl
Ortsliniengleichung[a+b==f, C] liefert eine Ellipse.
Was passiert, wenn die Strecke f kürzer oder länger ist?