Key Angles in the Unit Circle
- Author:
- Albert Navetta
- Topic:
- Angles, Circle, Unit Circle
Recall that for points on the unit circle, and . The figure below shows the unit circle with key angles marked and the cosine and sine of the angles in the first quadrant shown as the ordered pair of the terminal points on the unit circle. These angles and their sine and cosine should be committed to memory.
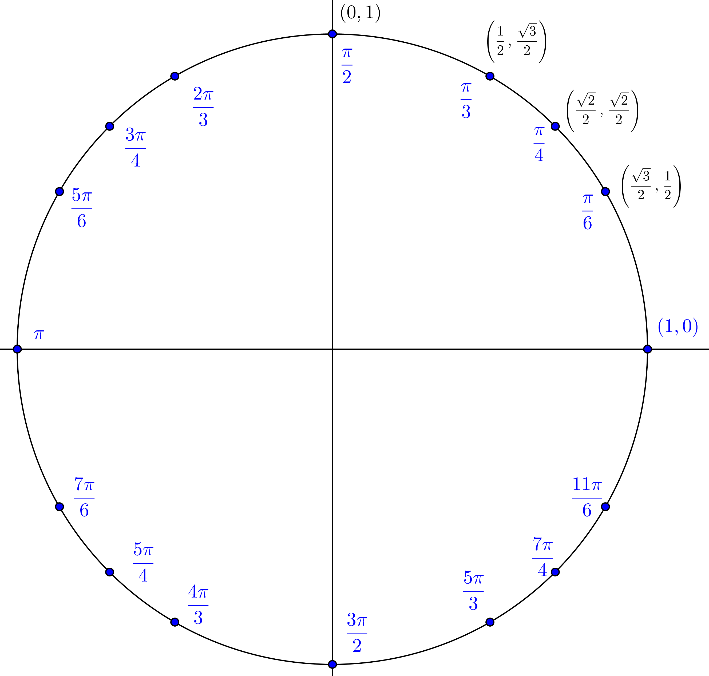
Why These Angles?
The angles shown are chosen because it is easy to calculate the exact values of sine and cosine. The angles who's terminal points are on the axes are obvious. For example and because the coordinates of the terminal point of are . Use a similar process to determine the sine and cosine of , and .
For the other angles in the first quadrant, The Pythagorean identity is used to calculate at least one of the values after the other is found. For example, if is known, calculate .
The on the right side is resolved by evaluating the quadrant of the angle. Since is the y-coordinate of the terminal point, is positive if the terminal point of is in quadrant I or II and negative in quadrant III or IV.
The interactive figure below shows how the sine and cosine of are known. The triangle shown is an equilateral triangle with each side equal to 1. Use the slider to move the triangle into the unit circle.
To show that , place an apex of the equilateral triangle at the origin and split the triangle in half along the positive x-axis as shown in the figure below. After that, the algebra to show that is exactly the same as the algebra showing that .
To show that , note that the terminal point of is the same distance from the x-axis and y-axis, therefore, . To find the value, use the Pythagorean identity . Since , the equation can be written
The terminal point of is in the first quadrant, so .