Corbes (II): equacions paramètriques i coordenades polars
Introducció
Ja hem vist com algunes corbes es poden expressar algebraicament o mitjançant construccions dinàmiques. Ara veurem com una mateixa corba es pot expressar en forma d'equació cartesiana, d'equacions paramètriques o en forma polar.
Lemniscata
La lemniscata és la corba determinada pel conjunt de punts del pla que compleixen que el producte de les distàncies a dos punts fixos és contant. Aquesta condició es pot expressar amb l'equació cartesiana:
(x2+y2)2 = 2a2 (x2-y2)
La corba té forma de "vuit horitzontal". És el símbol amb que representem l'infinit: ∞
Tasca 1
En una finestra nova de GeoGebra inseriu un punt lliscant a que prengui valors entre 0.1 i 4 amb un increment de 0.1. A la línia d'entrada escriviu: (x2+y2)2 = 2a2 (x2-y2).
Observeu que s'ha representat una lemniscata. Observeu com varia la corba en variar el paràmetre a.
Tasca 2
Igual que les equacions d'una recta es pot expressar en formes diferents: vectorial, paramètrica, contínua, general... Les corbes també es poden expressar de diverses formes. Hem vist la lemniscata expressada en forma cartesiana. Ara veurem com expressar-la en forma paramètrica.
Inseriu un punt lliscant t que prengui valors entre -pi i pi amb un increment de 0.1.
A la línia d'entrada escriviu:
i després:
Aquestes equacions es diuen paramètriques perquè cada punt ve determinat per un valor de t, és a dir, per a cada t tenim un punt de la corba i a cada punt de la corba li correspon un valor de t. En aquest cas t varia entre -pi i pi.
Inseriu a la línia d'entrada:
A=(coordx , coordy)
Activa el traç del punt A i l'animació de t.
Què hi observes? Quin paper juga el paràmetre a?
Tasca 3
GeoGebra incorpora un comandament que permet representar una corba a partir de les equacions paramètriques:
Coordenades polars
Hem començat el capítol de Geometria analítica comentant que donat un sistema de coordenades cartesià, tot punt quedava determinat per un parell de valors, anomenats coordenades, que indiquen quant a la dreta/esquerra i quant amunt/avall està situat respecte l'origen de coordenades.
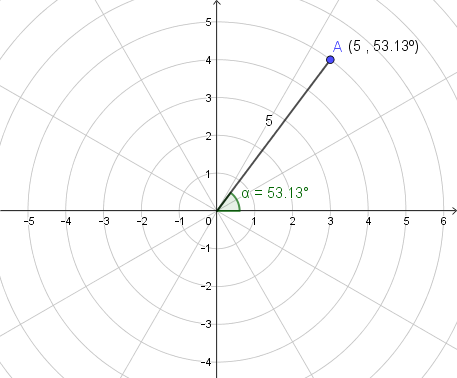
Aquesta no és l'única manera de localitzar un punt, també tenim les coordenades polars. Aquestes determinen a quina distància es troba de l'origen de coordenades i quin angle respecte el semieix positiu de les abscisses. Per exemple el punt A(4,3) en coordenades cartesianes és A(5 , 53.13º) en coordenades polars.
Si voleu veure la graella polar, heu de clicar amb el botó dret sobre la zona blanca de la finestra gràfica, trieu la darrera opció del menú, accediu a la pestanya Graella, seleccioneu Mostrar graella i el tipus Polar.
Tasca 4
Et proposem que resolgueu aquestes activitats amb llapis i paper:
a) un punt que té coordenades cartesianes (-3,4), quines coordenades polars tindrà?
b) un punt que té coordenades polars (2, 45º), quines coordenades cartesianes tindrà?
c) Troba unes fórmules que permetin passar d'un tipus de coordenades a l'altre.
Tasca 5
Obriu una finestra nova de GeoGebra. Inseriu un punt lliscant a que prengui valors entre 0.1 i 2 amb un increment de 0.1. Inseriu un punt lliscant t que prengui valors entre 0º i 360º amb un increment de 0,5º.
L'equació polar de la lemniscata, com podeu observar molt més senzilla:
Escriviu en la línia d'Entrada:
P=(sqrt(2a^2*cos(2t)) ; t) (observeu que hem posat ;)
Activeu el traç de P i l'animació de t.
Una altra forma per representar la lemniscata és:
Corba(sqrt(2*a^2*cos(2t))*cos(t), sqrt(2*a^2*cos(2t))*sin(t), t, 0º, 360º)
Saps d'on surt aquesta forma de representar-la?
Tasca 6
Accediu a aquesta pàgina web:
http://spaceweathergallery.com/indiv_upload.php?upload_id=102267
i observeu com el Sol descriu una corba similar a una lemniscata.
Per saber la relació entre la lemniscata i el Donut:
https://espiralcromatica.wordpress.com/tag/lemniscata-de-bernoulli/