Piyush Theorem
Piyush
PiyushTheorem: In a Right-Angled Triangle with sides in A.P. Series, the distance between the point of intersection of median & altitude at the base is 1/10 Th the sum of other two sides.
This Theorem applies in Two Conditions:
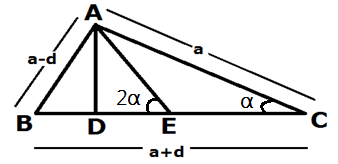 Tan α =AD/DC
AD= DC Tan α —————–1
Tan α = AD/DE
AD= DE Tan2 α —————-2
DC Tan α = DE Tan 2 α
(DE+EC) Tan α = DE Tan 2 α
DE Tan α + EC Tan α = DE Tan 2 α
DE Tan α + EC Tan α = 2 DE Tan α / (1- Tan2 α )
DE Tan α – DE Tan3 α + EC Tan α –EC Tan3 α = 2DE Tan α
EC Tan α –EC Tan3 α – DE Tan3 α = 2DE Tan α – DE Tan α
Tan α (EC – EC Tan2 α – DE T an2 α )= DE Tan α
DE Tan2 α – DE = EC Tan2 α – EC
-DE ( Tan2 α + 1) = -EC (1 – Tan2 α )
DE (sin2 α /cos2 α + 1) = EC (1- sin2 α /cos2 α )
DE (sin2 α + cos2 α /cos2 α ) = EC (cos2 α – sin2 α /cos2 α )
DE (sin2 α + cos2 α ) = EC(cos2 α –sin2 α )
DE (sin2 α + cos2 α ) = EC (cos2 α –sin2 α ) where (sin2 α + cos2 α =1) & (cos2 α –sin2 α = cos2 α ) DE= EC cos2 α
cos α =a/a+d & sin α = (a-d)/ (a +d)
cos2 α = a2/ (a +b) 2
sin2 α = (a-d) 2/ (a+ d) 2
DE= EC (cos2 α – sin2 α )
= EC (a2 / (a +b) 2 – (a-d) 2/ (a +d) 2
= EC (a2 – (a-d) 2/ (a +d) 2
= EC (a –a +d) (a+ a-d)/ (a+ d) 2
= EC (d) (2a -d)/ (a+ d) 2
= (a +d)/2(d) (2a -d)/ (a +d) 2 ————- where EC= (a +d)/2
= (d) (2a -d)/2(a +d)
= (d) (8d -d)/2(4d+d) ——————where a= 4d (as per the Theorem)
= 7d2 /2(5d)
= 7d /10
= (3d+4d)/10= (AB+AC)/10
Tan α =AD/DC
AD= DC Tan α —————–1
Tan α = AD/DE
AD= DE Tan2 α —————-2
DC Tan α = DE Tan 2 α
(DE+EC) Tan α = DE Tan 2 α
DE Tan α + EC Tan α = DE Tan 2 α
DE Tan α + EC Tan α = 2 DE Tan α / (1- Tan2 α )
DE Tan α – DE Tan3 α + EC Tan α –EC Tan3 α = 2DE Tan α
EC Tan α –EC Tan3 α – DE Tan3 α = 2DE Tan α – DE Tan α
Tan α (EC – EC Tan2 α – DE T an2 α )= DE Tan α
DE Tan2 α – DE = EC Tan2 α – EC
-DE ( Tan2 α + 1) = -EC (1 – Tan2 α )
DE (sin2 α /cos2 α + 1) = EC (1- sin2 α /cos2 α )
DE (sin2 α + cos2 α /cos2 α ) = EC (cos2 α – sin2 α /cos2 α )
DE (sin2 α + cos2 α ) = EC(cos2 α –sin2 α )
DE (sin2 α + cos2 α ) = EC (cos2 α –sin2 α ) where (sin2 α + cos2 α =1) & (cos2 α –sin2 α = cos2 α ) DE= EC cos2 α
cos α =a/a+d & sin α = (a-d)/ (a +d)
cos2 α = a2/ (a +b) 2
sin2 α = (a-d) 2/ (a+ d) 2
DE= EC (cos2 α – sin2 α )
= EC (a2 / (a +b) 2 – (a-d) 2/ (a +d) 2
= EC (a2 – (a-d) 2/ (a +d) 2
= EC (a –a +d) (a+ a-d)/ (a+ d) 2
= EC (d) (2a -d)/ (a+ d) 2
= (a +d)/2(d) (2a -d)/ (a +d) 2 ————- where EC= (a +d)/2
= (d) (2a -d)/2(a +d)
= (d) (8d -d)/2(4d+d) ——————where a= 4d (as per the Theorem)
= 7d2 /2(5d)
= 7d /10
= (3d+4d)/10= (AB+AC)/10
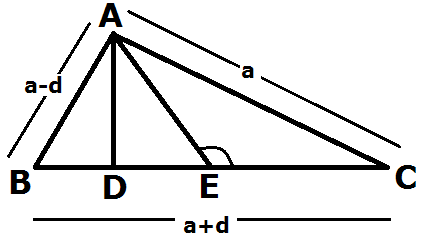 AC2=EC2 +AE2 +2CE.DE where EC = ( a +d) /2,AE=( a +d)/2
a2 = (a +d/2)2 + (a+ d/2)2 + 2(a +d)/2DE
= (a +d/2) (a+d+2DE)
= (a +d/2) (a+d+2DE) where a=4d
16d2 = (5d/2) (5d+2DE)
32d/5 = 5d + 2DE
32d/5 – 5d = 2DE
32d -25d/5 = 2DE
DE =7d/10
= (3d+4d)/10 = (AB+AC)/10
AC2=EC2 +AE2 +2CE.DE where EC = ( a +d) /2,AE=( a +d)/2
a2 = (a +d/2)2 + (a+ d/2)2 + 2(a +d)/2DE
= (a +d/2) (a+d+2DE)
= (a +d/2) (a+d+2DE) where a=4d
16d2 = (5d/2) (5d+2DE)
32d/5 = 5d + 2DE
32d/5 – 5d = 2DE
32d -25d/5 = 2DE
DE =7d/10
= (3d+4d)/10 = (AB+AC)/10
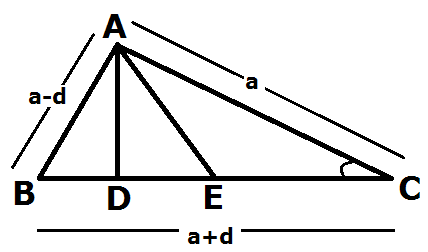 AB2= AC2+BC2 – 2BC.DC
(a-d) 2= a2 + (a+ d) 2 -2(a+ d) (DE+EC) where AB= (a-d), AC=a, BC =( a +d) & EC= (a +d)/2
(a-d) 2 – (a +d)2 = a2 -2(a +d)(DE+EC)
(a- d –a-d) (a -d +a +d) = a2 -2(a+ d) (2DE+a+d)/2
2(-2d) (2a) = 2a2 -2(a +d) (2DE+a+d)
-8ad – 2a2 = -2(a +d) (2DE+a+d)
-2a (4d +a) = -2(a +d) (2DE+a+d)
a (4d + a) = (a +d)(2DE+a+d)
4d (4 d + 4d) = (4d+d) (2DE+4d+d)
4d (8d) = (5d) (2DE+5d)
32d2/5d = (2DE+5d)
32d/5 = (2DE+5d)
32d/5 – 5d = 2DE
(32d – 25d)/5 = 2 DE
DE = 7d/10
= (3d+4d)/10 = (AB+AC)/10
4. Proof with Co-ordinates Geometry
AB2= AC2+BC2 – 2BC.DC
(a-d) 2= a2 + (a+ d) 2 -2(a+ d) (DE+EC) where AB= (a-d), AC=a, BC =( a +d) & EC= (a +d)/2
(a-d) 2 – (a +d)2 = a2 -2(a +d)(DE+EC)
(a- d –a-d) (a -d +a +d) = a2 -2(a+ d) (2DE+a+d)/2
2(-2d) (2a) = 2a2 -2(a +d) (2DE+a+d)
-8ad – 2a2 = -2(a +d) (2DE+a+d)
-2a (4d +a) = -2(a +d) (2DE+a+d)
a (4d + a) = (a +d)(2DE+a+d)
4d (4 d + 4d) = (4d+d) (2DE+4d+d)
4d (8d) = (5d) (2DE+5d)
32d2/5d = (2DE+5d)
32d/5 = (2DE+5d)
32d/5 – 5d = 2DE
(32d – 25d)/5 = 2 DE
DE = 7d/10
= (3d+4d)/10 = (AB+AC)/10
4. Proof with Co-ordinates Geometry
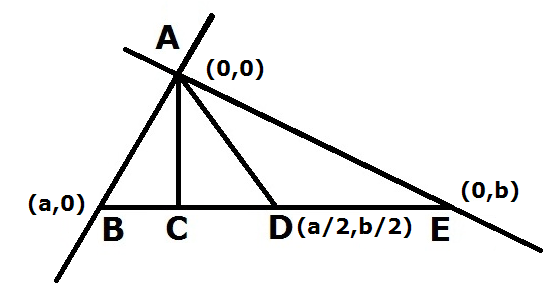 Equation of BE
Y – 0 =b-0/0-a(X – a)
Y = -b/a(X) + b——————- (1)
M1 = -b/a
For perpendicular
M1M2= -1
So M2=a/b
Equation of AC
Y – 0 = a/b(X-0)
Y=a/b(X) —————— (2)
Put Y value in equation (1)
a/b(X) + b/a(X) =b
X (a2+b2/a b) = b
X = ab2/ (a2 + b2)
To get Value of Y, put X value in equation (2)
Y = a/b (ab2/ (a2+b2)
Y = a2b/ (a2+b2)
Here we got co-ordinates of Point C – ab2/ (a2 + b2), a2b/ (a2+b2) and co-ordinates of point d is (a/2, b/2) because d is midpoint.
As per the “Theorem” a=z-d, b=z, c = z+ d
(z +d) 2= (z-d) 2+z2 from here z=4d so a=3d and b=4d
Put value of a & b
ab2/ (a2 + b2), a2b/ (a2+b2) & (a/2, b/2)
ab2/ (a2 + b2) = 48d/25
a2b/ (a2+b2) = 36d/25
a/ 2=3d/2
b/ 2 =4d/2
CD2= (48d/25 -3d/2)2-(36d/25-4d/2)2
= (96d-75d/50)2 + (72d-100d/50)2
= (21d/50)2 + (-28d/50)2
= (441d2/2500) + (784d2/2500)
= (1225d2/2500)
CD= 35d/50 = 7d/10
= 7d/10 = (3d+4d)/10 = (AB+AE)/10
www.piyushgoel.in
Equation of BE
Y – 0 =b-0/0-a(X – a)
Y = -b/a(X) + b——————- (1)
M1 = -b/a
For perpendicular
M1M2= -1
So M2=a/b
Equation of AC
Y – 0 = a/b(X-0)
Y=a/b(X) —————— (2)
Put Y value in equation (1)
a/b(X) + b/a(X) =b
X (a2+b2/a b) = b
X = ab2/ (a2 + b2)
To get Value of Y, put X value in equation (2)
Y = a/b (ab2/ (a2+b2)
Y = a2b/ (a2+b2)
Here we got co-ordinates of Point C – ab2/ (a2 + b2), a2b/ (a2+b2) and co-ordinates of point d is (a/2, b/2) because d is midpoint.
As per the “Theorem” a=z-d, b=z, c = z+ d
(z +d) 2= (z-d) 2+z2 from here z=4d so a=3d and b=4d
Put value of a & b
ab2/ (a2 + b2), a2b/ (a2+b2) & (a/2, b/2)
ab2/ (a2 + b2) = 48d/25
a2b/ (a2+b2) = 36d/25
a/ 2=3d/2
b/ 2 =4d/2
CD2= (48d/25 -3d/2)2-(36d/25-4d/2)2
= (96d-75d/50)2 + (72d-100d/50)2
= (21d/50)2 + (-28d/50)2
= (441d2/2500) + (784d2/2500)
= (1225d2/2500)
CD= 35d/50 = 7d/10
= 7d/10 = (3d+4d)/10 = (AB+AE)/10
www.piyushgoel.in
- The Triangle must be Right-Angled.
- Its Sides are in A.P. Series.
- Proof with Trigonometry
- Proof with Obtuse Triangle Theorem
- Proof with Acute Triangle Theorem