Wie rechnet man denn sowas?
Punkte und Geraden mit ihren Gleichungen werden in homogenen Koordinaten und dargestellt.
Das Skalarprodukt kann man als Linearform in Punktkoordinaten oder als Linearform in Geradenkoordinaten lesen.
; vorausgesetzt, die Punkte befinden sich in "allgemeiner Lage", dh. keine 3 der fünf Punkte liegen auf einer Geraden.
Vertauscht man die Rolle von Geraden und Punkten, so ergibt sich:
Fazit: 5 Geraden sind Tangenten eines eindeutig bestimmten Kegelschnitts, sofern die Geraden sich in allgemeiner Lage befinden, dh. keine 3 der 5 Geraden gehen durch einen gemeinsamen Punkt. Die oben beschriebene Rechenmethode liefert die Quadrik für die Geradenvektoren, gesucht ist die zugehörige Quadrik für die Berührpunkte. Eine symmetrische Bilinearform läßt sich beschreiben durch eine symmetrische Matrix : . Ist die symmetrische Matrix für die Quadrik der Berührgeraden, so ist die symmetrische Matrix für die Berührpunktvektoren.
Die Matrix erhält man, indem man in die Bilinearform die Einheitsvektoren einsetzt: . Diese Matrix muss man invertieren, um die Quadrik für die Tangentenberührpunkte zu berechnen.
Zu 4 Punkten und einer Geraden diejenigen Kegelschnitte durch die Punkte berechnen, welche die Gerade berühren:
Die einzelnen Kegelschnitte des Kegelschnittbüschels durch die 4 Punkte schneiden in der Regel die Gerade in 2 Punkten. Setzt man die Punkte der Geraden mit 2 verschiedenen Punkten der Geraden in die quadratische Form ein, so erhält man eine quadratische Gleichung für die Schnittpunkte der Geraden mit dem Kegelschnitt.
Bekanntlich gibt es nur eine Lösung, und der zugehörige Punkt ist dann Berührpunkt, wenn die Diskriminante der quadratischen Gleichung Null ist. In der Diskriminante kommt quadratisch vor, also ist eine quadratische Gleichung für , die Lösungen liefern die 2 Berührkegelschnitte.
Die Rechnungen für 4 Geraden und einen Punkt verlaufen dual. Auch hier muss man wieder zusätzlich die Inverse der symmetrischen Bilinearform-Matrix bestimmen.
Zu unserer anfänglichen Verblüffung erwiesen sich einige inverse Matrizen als Null-Matrix. Des Rätsels Lösung rührt an ein Problem der Rechengenauigkeit: die Vektoren sind für die Rechnungen nicht normiert, nach mehreren Kreuzprodukten können sich die Koeffizienten zu beachtlicher Größe aufschaukeln, beim Invertieren erhält man dann bei einer Voreinstellung der Ausgabegenauigkeit mit 2 Nachkommastellen schnell einmal eine Null-Matrix, die das eigentlich nicht ist.
Mit unserem veralteten CAS-Programm Derive wurden die Rechnungen blitzschnell exakt ausgegeben, die Lösungen konnten dann manchmal radikal etwa wie aussehen, dh. mit Wurzeln und Brüchen, was bei Eingabe von nur rationalen Zahlen möglich ist, wenn zur Berechnung allenfalls quadratische Gleichungen zu lösen sind.
Überhaupt erlaubte dieses "veraltete" CAS-Programm durch Verwendung von Funktionen, deren Variablen- und Ausgabe-Typ nicht spezifiziert werden muss, die Rechenwerkzeuge für die Kegelschnittwerkzeuge auf wenige effektive Zeilen zu beschränken.
Da unsere früheren Erfahrungen mit der GeGebra-CAS geprägt sind durch zahlreiche Abstürze und extreme Verlangsamung geometrischer Aktivitäten, haben wir den Einsatz von GeGebra-CAS für die Kegelschnitt-Werkzeuge vermieden, dh. nicht getestet.
Literatur:
Die Grundlagen für die Berechnungen findet man in dem in Blatt1 genannten Buch Geometriekalküle von J. Richter-Gebert und Th. Orendt.
Unten sind die Derive-Funktionen aufgeführt, die aus einer Matrix M aus 5 Punkten in homogenen Koordinaten die Kegelschnittgleichung für den Kegelschnitt durch die 5 Punkte berechnet.
- Ein Punkt liegt auf , bzw. geht durch , wenn gilt.
- Der Schnittpunkt zweier Geraden ist , wobei das Kreuzprodukt bezeichnet
- Die Verbindungsgerade zweier Punkte ist
; vorausgesetzt, die Punkte befinden sich in "allgemeiner Lage", dh. keine 3 der fünf Punkte liegen auf einer Geraden.
Vertauscht man die Rolle von Geraden und Punkten, so ergibt sich:
Fazit: 5 Geraden sind Tangenten eines eindeutig bestimmten Kegelschnitts, sofern die Geraden sich in allgemeiner Lage befinden, dh. keine 3 der 5 Geraden gehen durch einen gemeinsamen Punkt. Die oben beschriebene Rechenmethode liefert die Quadrik für die Geradenvektoren, gesucht ist die zugehörige Quadrik für die Berührpunkte. Eine symmetrische Bilinearform läßt sich beschreiben durch eine symmetrische Matrix : . Ist die symmetrische Matrix für die Quadrik der Berührgeraden, so ist die symmetrische Matrix für die Berührpunktvektoren.
Die Matrix erhält man, indem man in die Bilinearform die Einheitsvektoren einsetzt: . Diese Matrix muss man invertieren, um die Quadrik für die Tangentenberührpunkte zu berechnen.
Zu 4 Punkten und einer Geraden diejenigen Kegelschnitte durch die Punkte berechnen, welche die Gerade berühren:
Die einzelnen Kegelschnitte des Kegelschnittbüschels durch die 4 Punkte schneiden in der Regel die Gerade in 2 Punkten. Setzt man die Punkte der Geraden mit 2 verschiedenen Punkten der Geraden in die quadratische Form ein, so erhält man eine quadratische Gleichung für die Schnittpunkte der Geraden mit dem Kegelschnitt.
Bekanntlich gibt es nur eine Lösung, und der zugehörige Punkt ist dann Berührpunkt, wenn die Diskriminante der quadratischen Gleichung Null ist. In der Diskriminante kommt quadratisch vor, also ist eine quadratische Gleichung für , die Lösungen liefern die 2 Berührkegelschnitte.
Die Rechnungen für 4 Geraden und einen Punkt verlaufen dual. Auch hier muss man wieder zusätzlich die Inverse der symmetrischen Bilinearform-Matrix bestimmen.
Zu unserer anfänglichen Verblüffung erwiesen sich einige inverse Matrizen als Null-Matrix. Des Rätsels Lösung rührt an ein Problem der Rechengenauigkeit: die Vektoren sind für die Rechnungen nicht normiert, nach mehreren Kreuzprodukten können sich die Koeffizienten zu beachtlicher Größe aufschaukeln, beim Invertieren erhält man dann bei einer Voreinstellung der Ausgabegenauigkeit mit 2 Nachkommastellen schnell einmal eine Null-Matrix, die das eigentlich nicht ist.
Mit unserem veralteten CAS-Programm Derive wurden die Rechnungen blitzschnell exakt ausgegeben, die Lösungen konnten dann manchmal radikal etwa wie aussehen, dh. mit Wurzeln und Brüchen, was bei Eingabe von nur rationalen Zahlen möglich ist, wenn zur Berechnung allenfalls quadratische Gleichungen zu lösen sind.
Überhaupt erlaubte dieses "veraltete" CAS-Programm durch Verwendung von Funktionen, deren Variablen- und Ausgabe-Typ nicht spezifiziert werden muss, die Rechenwerkzeuge für die Kegelschnittwerkzeuge auf wenige effektive Zeilen zu beschränken.
Da unsere früheren Erfahrungen mit der GeGebra-CAS geprägt sind durch zahlreiche Abstürze und extreme Verlangsamung geometrischer Aktivitäten, haben wir den Einsatz von GeGebra-CAS für die Kegelschnitt-Werkzeuge vermieden, dh. nicht getestet.
Literatur:
Die Grundlagen für die Berechnungen findet man in dem in Blatt1 genannten Buch Geometriekalküle von J. Richter-Gebert und Th. Orendt.
Unten sind die Derive-Funktionen aufgeführt, die aus einer Matrix M aus 5 Punkten in homogenen Koordinaten die Kegelschnittgleichung für den Kegelschnitt durch die 5 Punkte berechnet.
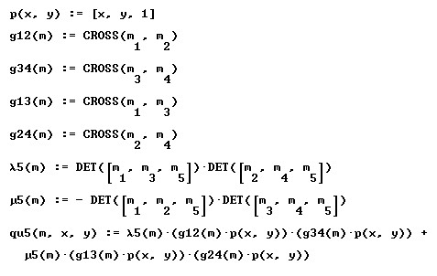
Dieses Arbeitsblatt ist Teil des Geogebrabooks Kegelschnitt-Werkzeuge