Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

IM1H 6.3 Part 2

Author:Julie Silverwood, aeichman, Amy Springstead

Quadrilateral Toolkit

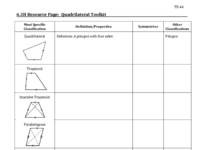
Quadrilateral Toolkit.pdf

Quadrilateral Toolkit.pdf

A line that reflects a figure onto itself is called a line of symmetry. A figure that can be carried onto itself by a rotation is said to have rotational symmetry. A diagonal of a polygon is any line segment that connects non-consecutive vertices of the polygon. For each of the below regular polygons, describe the rotations and reflections that carry it onto itself. Be as specific as possible in your descriptions, such as specifying the angle of rotation.

1. What angles of rotation does the triangle have? How many lines of reflection does the triangle have?

2. What angles of rotation does the square have? How many lines of reflection does the square have?

3. What angles of rotation does the pentagon have? How many lines of reflection does the pentagon have?

4. What angles of rotation does the hexagon have? How many lines of reflection does the hexagon have?

5. What angles of rotation does the octagon have? How many lines of reflection does the octagon have?

6. What angles of rotation does the nonagon have? How many lines of reflection does the nonagon have?

7. What patterns do you notice in terms of the number and characteristics of the lines of symmetry in a regular polygon. (Hint: think about even versus odd)

8. What patterns do you notice in terms of the angles of rotation when describing the rotational symmetry in a regular polygon?

Reflection

What are the main things you want to remember from this task?

Quadrilaterals Quizlet

Quadrilaterals Quizlet

Quadrilaterals Quizlet

https://quizlet.com/_2wyy1x

New Resources

Discover Resources

Discover Topics