What is the Locus of a point that moves in such a way that it's sum of the squares of the distance (with weight factors) to N fixed points remains constant?
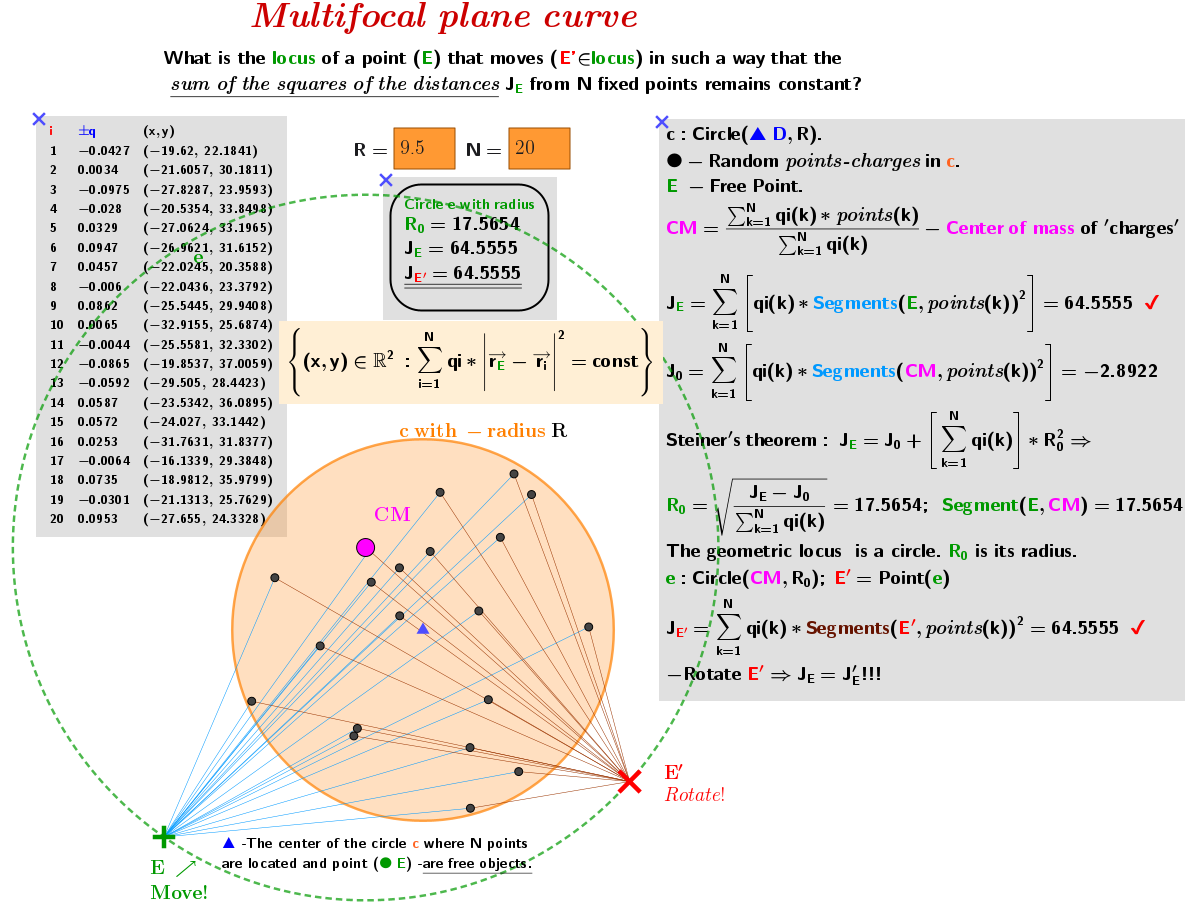
What is the Locus of a point E that E' moves in such a way that it's sum of the squares of the distance (with weight factors) to N fixed points remains constant?
Use Applet to visualize that in this case the locus of points is a circle (regardless of the number and location of N points) with center at the center of "mass" (CM) of the system of "charged" points and radius R0 calculated by the given formula.
The algebraic sum of squares of distances: qi*|x - xi|² is taken with weighting factors qi by analogy with electrostatic charges.
*Click the Update button until a green circle appears in the plane of the screen.
For a given set of N points and a point E such that the sum of the squares of the distances with weight factors (the blue segments) is JE, check that JE'=JE and remains unchanged for a moving point E' belonging to the locus-circle (the brown segments connect E' to the N points).
Example of distribution of charged particles