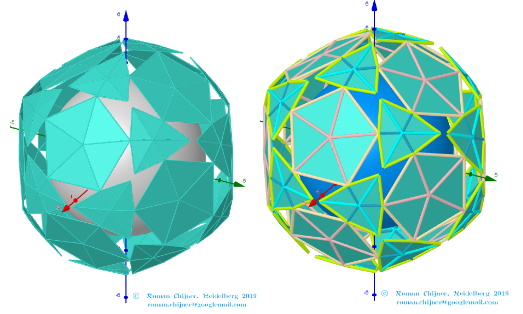
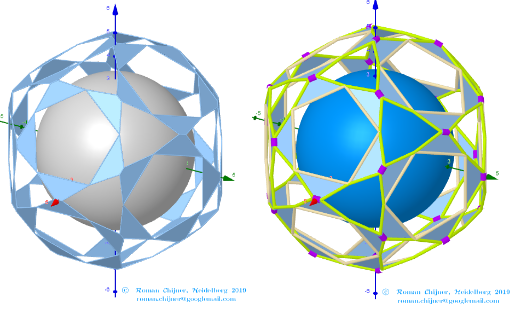
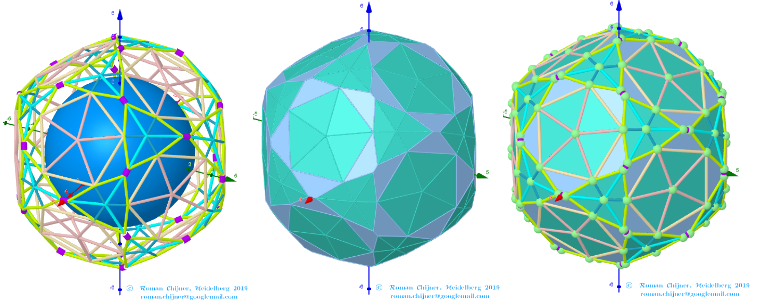
Images . Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of a trisection of its 10th-order segments
Generating Elements of mesh modeling the surfaces of polyhedron, its dual image and the coloring of their edges and faces can be found in the applet.

Elements in polyhedron Biscribed Pentakis Dodecahedron(10)
Vertices: V = 120.
Faces: F =152. 80{3}+60{4}+12{5}
Edges: E =270. 120+30+60+60 - The order of the number of edges in this polyhedron are according to their length.
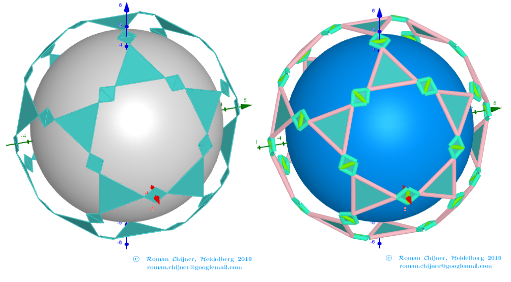
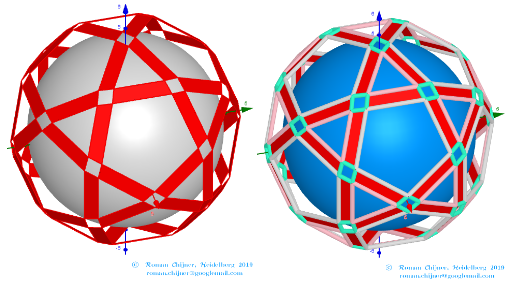
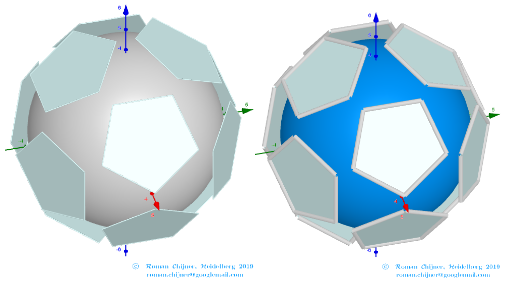
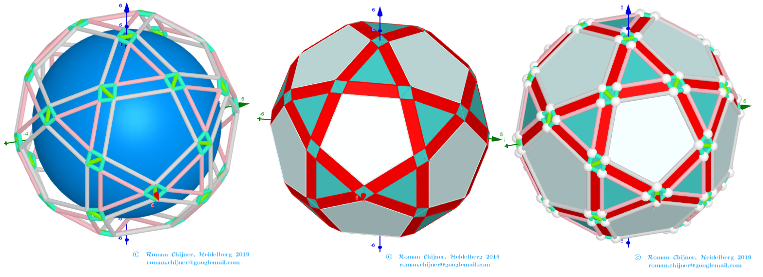
The elements of the dual to the Biscribed Pentakis Dodecahedron(10)
Vertices: V = 152.
Faces: F =240. 180{3}+60{4}
Edges: E =390. 30+60+120+60+60+60- The order of the number of edges in this polyhedron are according to their length.