Posizioni reciproche tra retta e circonferenza
Prepariamo il foglio di Geogebra
Dopo aver eliminato gli assi cartesiani [tasto destro mouse su finestra grafica: Assi] e attivato la griglia [tasto destro mouse su finestra grafica: Griglia] iniziamo.
ESERCIZIO N°1
- Tracciamo una circonferenza sul piano: disegniamo un punto sul piano che sarà il nostro centro
 e rinominiamolo con O (tasto destro sul punto: Rinomina]. Tracciamo una circonferenza di centro O e per un punto a piacere
e rinominiamolo con O (tasto destro sul punto: Rinomina]. Tracciamo una circonferenza di centro O e per un punto a piacere 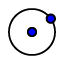 ; rinominiamo tale punto con C.
; rinominiamo tale punto con C.
- Disegniamo due punti esterni alla circonferenza
 che rinomineremo con P e Q. Tracciamo la retta per P e Q
che rinomineremo con P e Q. Tracciamo la retta per P e Q 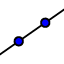
- Muoviamo
 il punto Q in modo che la retta incontri la circonferenza in due punti. Individuiamo tali punti di intersezione con il comando intersezione
il punto Q in modo che la retta incontri la circonferenza in due punti. Individuiamo tali punti di intersezione con il comando intersezione  . Rinominiamo tali punti con A e B.
. Rinominiamo tali punti con A e B. - Muoviamo il punto Q
 e osserviamo il comportamento dei punti A e B.
e osserviamo il comportamento dei punti A e B.
Riassumiamo le osservazioni svolte
Una retta è esterna quando
Una retta è tangente quando
Una retta è secante quando
ESERCIZIO N°2
Proviamo adesso a caratterizzare in altro modo il fatto che la retta è esterna, tangente o secante.
- Traccia una circonferenze di diametro
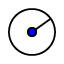 fisso di 4cm e con centro O.
fisso di 4cm e con centro O. - Traccia una retta esterna
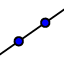
- Misuriamo il raggio della nostra circonferenza. Utilizziamo il comando
 distanza [che troviamo nel menù degli angoli]: scegliamo il punto O e il punto C.
distanza [che troviamo nel menù degli angoli]: scegliamo il punto O e il punto C. - Ora misuriamo la distanza delle rette dal centro O della circonferenze. Utilizziamo lo stesso comando
 scegliendo il centro O e la retta r.
scegliendo il centro O e la retta r. - Muoviamo
 la retta spostando Q. Cosa possiamo osservare riguardo alla distanza della retta da O rispetto al raggio?
la retta spostando Q. Cosa possiamo osservare riguardo alla distanza della retta da O rispetto al raggio?
 Teorema
Se la retta r è esterna alla circonferenza allora la distanza della retta dal centro O della circonferenza è
Teorema
Se la retta r è esterna alla circonferenza allora la distanza della retta dal centro O della circonferenza è
 Teorema
Se la retta r è tangente alla circonferenza allora la distanza della retta dal centro O della circonferenza è
Teorema
Se la retta r è tangente alla circonferenza allora la distanza della retta dal centro O della circonferenza è
 Teorema
Se la retta r è secante alla circonferenza allora la distanza della retta dal centro O della circonferenza è
Teorema
Se la retta r è secante alla circonferenza allora la distanza della retta dal centro O della circonferenza è
 Teorema
Se la retta r è secante alla circonferenza allora la distanza della retta dal centro O della circonferenza è
Teorema
Se la retta r è secante alla circonferenza allora la distanza della retta dal centro O della circonferenza è
 Teorema
Se la retta r è tangente alla circonferenza allora quanti punti hanno in comune la retta e la circonferenza?
Teorema
Se la retta r è tangente alla circonferenza allora quanti punti hanno in comune la retta e la circonferenza?
ESPLORAZIONE N°1
| Traccia un punto A nel piano e una retta con distanza di 4 unità da P. Quante rette con questa caratteristica puoi tracciare? Utilizza il foglio di geogebra qui di seguito |
ESPLORAZIONE N°2
Traccia un segmento AB lungo 4 unità
| • Disegna la perpendicolare al segmento AB passante per B: è una retta che dista 4 unità da A • Clicca con il tasto destro del mouse sulla retta e scegli “Traccia attiva” • Trascina il punto B, vengono tracciate le infinite rette che distano 4 unità da A; come puoi notare, il loro insieme (che si chiama INVILUPPO) disegna nel piano una circonferenza di centro A e raggio 4 unità |
| ESPLORAZIONE N°3 |
| Due ruote dentate, una con raggio di 2 unità, l’altra con raggio di 3 unità, devono ingranare con una terza con raggio di 4 unità. La distanza tra i centri delle prime due ruote è di 7 unità. Come posizioneresti le tre ruote? |
ESPLORAZIONE N°4
Osserva i tre punti inseriti nel piano cartesiano.
Trova le coordinate del punto che soddisfa contemporaneamente le tre condizioni di seguito riportate
- a distanza di 13 unità/cm da C
- a distanza di 10 u da B
- a distanza di 6 u da D