Transformación de funciones
Desplazamientos y amplificaciones
Vamos a estudiar como se transforma la gráfica de una función cuando realizamos las siguientes operaciones:
- Desplazamiento vertical: , comprueba como al variar , la función se desplaza verticalmente, dicha cantidad. Si , el desplazamiento es hacia arriba y en caso contrario hacia abajo
- Desplazamiento horizontal: Se puede presentar de dos formas, o , solo varía el signo, por tanto habrá que tener cuidado a la hora de su interpretación, en este caso se ha tomado , es decir. cuando , el desplazamiento es hacia la derecha, y en caso contrario hacia la izquierda (al revés si hubiéramos tomado la segunda expresión
- Amplificación vertical: , Si , la función se "estira" verticalmente, en caso contrario se "contrae" verticalmente. Si la constante es negativa. se transforma en opuesta, y si es 0, no tiene sentido, porque nos quedaría la función
- Amplificación horizontal: Si la función se "contrae" horizontalmente, en caso contrario se "estira" horizontalmente. Si la constante es negativa. se transforma en opuesta, y si es 0, no tiene sentido, porque nos quedaría la expresión
Puedes introducir la expresión que quieras e ir visualizando las acciones en cada uno de los casos, modificando las constantes y comprobando su efecto en la gráfica de la función.
Calculadora de transformaciones
Ahora podrás comprobar cómo varía la gráfica de una función cuando le aplicas varias transformaciones
Puedes introducir cualquier función e ir modificando las constantes para observar la variación
A modo de ejemplo: Prueba con , y transfórmala en
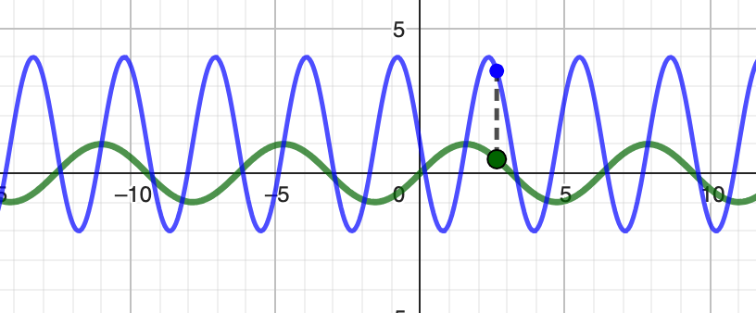
¿Qué ha ocurrido?
- El -3 de delante hace que la amplitud de la función seno sea de -3 a 3 y además al ser negativo invierte el signo de la función, el 2 ha hecho que el periodo de reduzca a la mitad (se ha "contraído") y el 1 ha desplazado la función una unidad hacia arriba