Lesson 15-16 ~ Optional
LESSON 15The Volume of a ConeLearning goalsLearning goals(Student Facing)Learning targets(Student Facing)Required PreparationPrint-Formatted Word DocumentsPrint-Formatted PDFsIn this lesson students start working with cones, and learn that the volume of a cone is 13 the volume of a cylinder with a congruent base and the same height. First, students learn a method for quickly sketching a cone, and the meaning of the radius and height of a cone. Then they watch a video (or if possible, a live demonstration) showing that it takes three cones of water to fill a cylinder with the same radius and height. At this point, it is taken as a mysterious and beautiful fact that the volume of a cone is one third the volume of the associated cylinder. A proof of this fact requires mathematics beyond grade level.Students write the volume of a cone given a specific volume of a cylinder with the same base and height, and vice versa. Then they use the formula for the volume of a cylinder learned in previous lessons to write the general formula V=13πr2h for the volume, V, of a cone in terms of its height, h, and radius, r. Finally, students practice computing the volumes of some cones. There are opportunities for further practice in the next lesson.CCSS Standards: AddressingWARM-UP: 5 minutes15.1: Which Has a Larger Volume?Instructional RoutinesCCSS Standards: AddressingThe purpose of this activity is for students to think about how the volume of a cone might relate to the volume of a cylinder with the same base and height. Additionally, students learn one method for sketching a cone. In this activity, just elicit students’ best guess about how many cone-contents would fit into the cylinder (or, what fraction of the cylinder’s volume is the cone’s volume). In the next activity, they will watch a demonstration that verifies the actual amount.LaunchIf you have access to appropriate geometric solids that include a cylinder and a cone with congruent bases and equal heights, consider showing these to students, even passing them around for students to hold if time permits.Arrange students in groups of 2. Give students 2–3 minutes of quiet work time, followed by time to discuss fractional amount with partner. Follow with a whole-class discussion.Conceptual Processing: Manipulatives. Provide manipulatives (i.e., geometric solids) to aid students who benefit from hands-on activities.Student-Facing Task StatementThe cone and cylinder have the same height, and the radii of their bases are equal.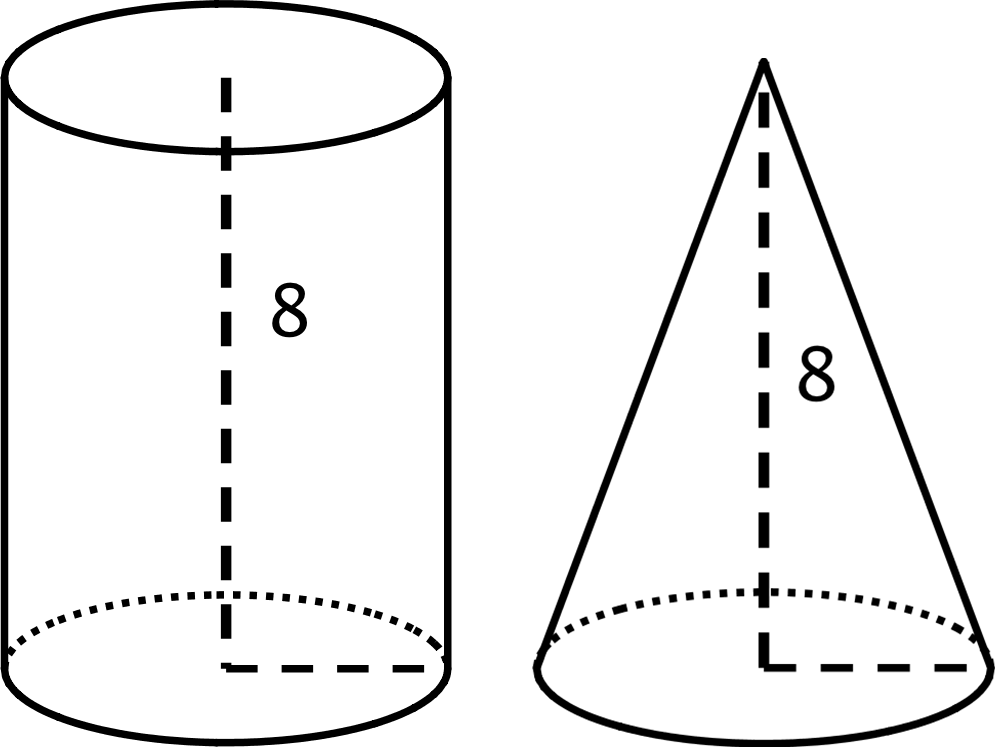
 ACTIVITY: 20 minutes15.2: From Cylinders to ConesInstructional RoutinesCCSS Standards: AddressingIn this activity, students use the relationship that the volume of a cone is 13 of the volume of a cylinder to calculate the volume of various cones. Students start by watching a video (or demonstration) that shows that it takes the contents of 3 cones to fill the cylinder when they have congruent bases and equal heights. Students use this information to calculate the volume of various cones and cylinders. For the last question, identify students who:
ACTIVITY: 20 minutes15.2: From Cylinders to ConesInstructional RoutinesCCSS Standards: AddressingIn this activity, students use the relationship that the volume of a cone is 13 of the volume of a cylinder to calculate the volume of various cones. Students start by watching a video (or demonstration) that shows that it takes the contents of 3 cones to fill the cylinder when they have congruent bases and equal heights. Students use this information to calculate the volume of various cones and cylinders. For the last question, identify students who: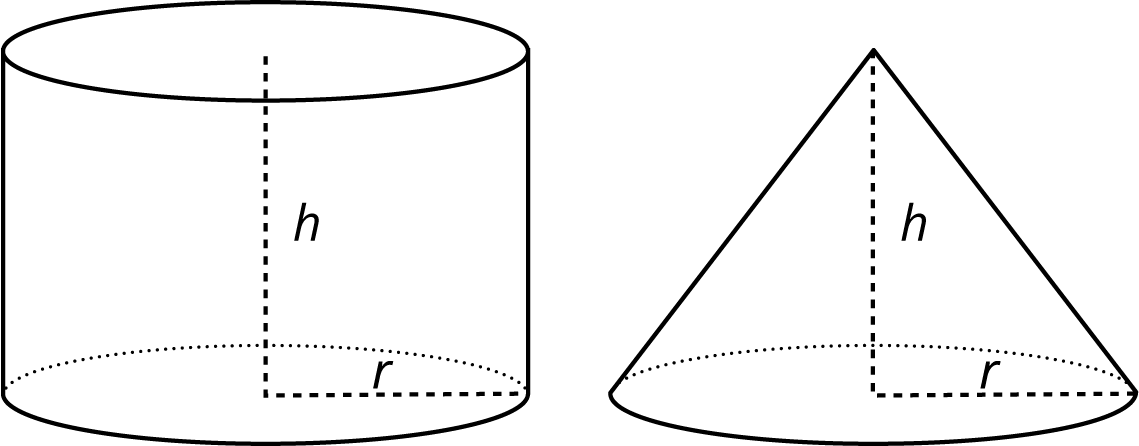 A cone and cylinder have the same height and their bases are congruent circles.
A cone and cylinder have the same height and their bases are congruent circles.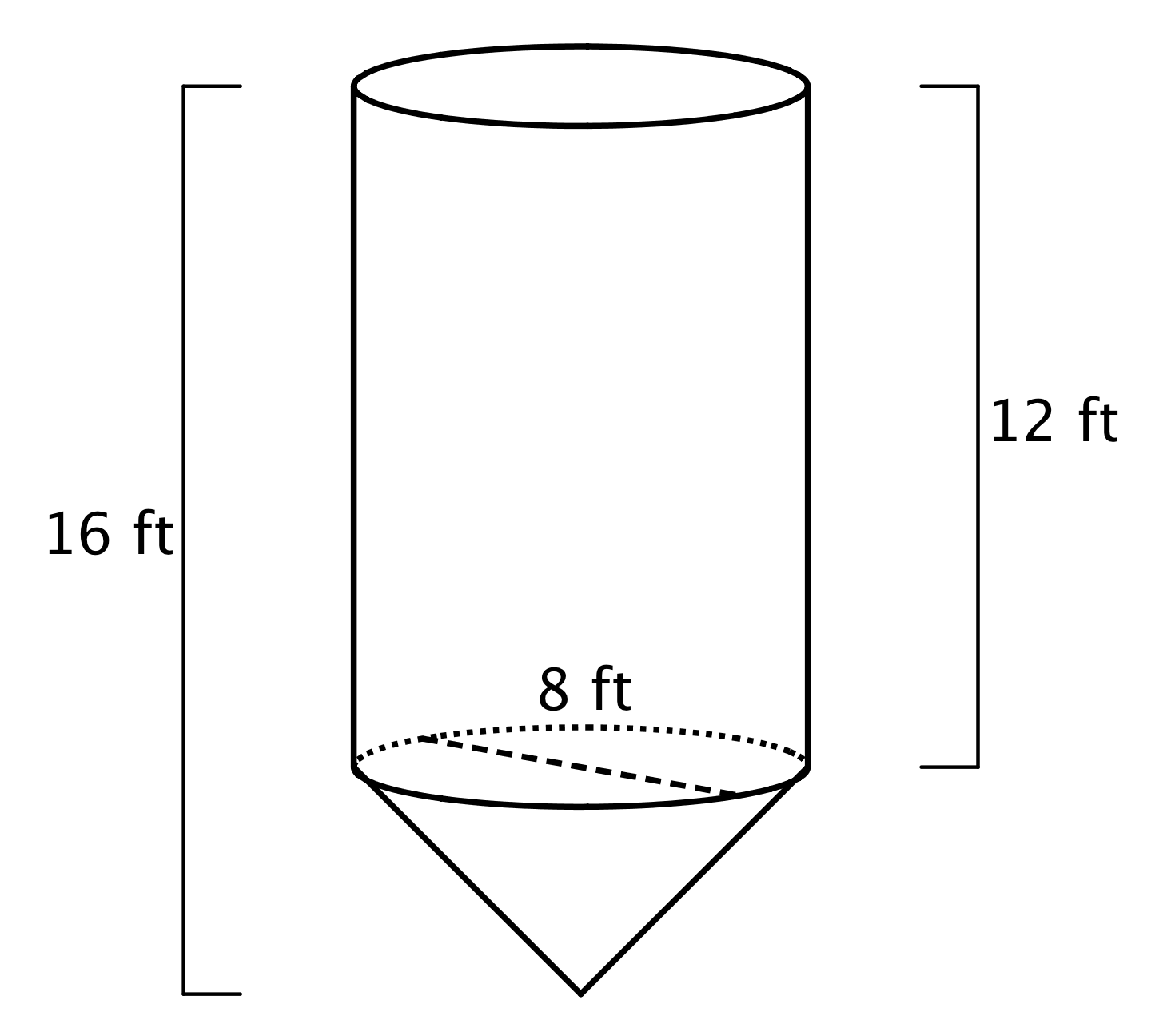 "Are you ready for more?" Student ResponseThe entire grain silo holds 6403π cubic feet of grain.The cone holds 643π cubic feet of grain. Since the radius is 4 feet and the height of the cone is also 4 feet (16−12), the volume is 13π42⋅4. Calculate the volume of the cylinder (π42⋅12), and add it to the volume of the cone to get the volume of the entire silo. Activity SynthesisFor the first problem, Invite students to explain how they calculated the volume of both figures and have them share the different strategies they used. If not mentioned by students bring up these strategies:
"Are you ready for more?" Student ResponseThe entire grain silo holds 6403π cubic feet of grain.The cone holds 643π cubic feet of grain. Since the radius is 4 feet and the height of the cone is also 4 feet (16−12), the volume is 13π42⋅4. Calculate the volume of the cylinder (π42⋅12), and add it to the volume of the cone to get the volume of the entire silo. Activity SynthesisFor the first problem, Invite students to explain how they calculated the volume of both figures and have them share the different strategies they used. If not mentioned by students bring up these strategies: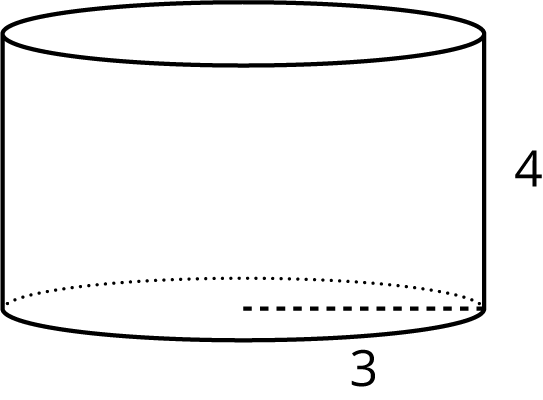 Student Responsecylinder: 36π cubic units because π⋅32⋅4=36πcone: 36π cubic units because 13π⋅32⋅12=36π
Student Responsecylinder: 36π cubic units because π⋅32⋅4=36πcone: 36π cubic units because 13π⋅32⋅12=36π
- Which figure has a larger volume?
- Do you think the volume of the smaller one is more or less than 12 the volume of the larger one? Explain your reasoning.

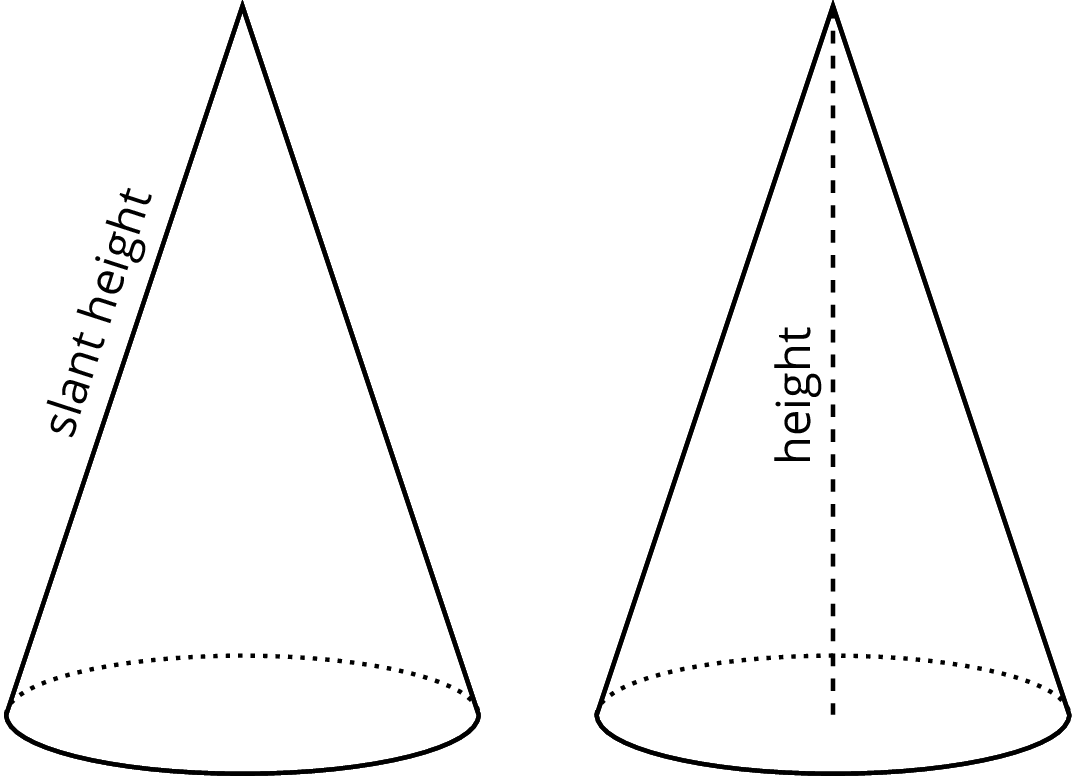
- Here is a method for quickly sketching a cone:
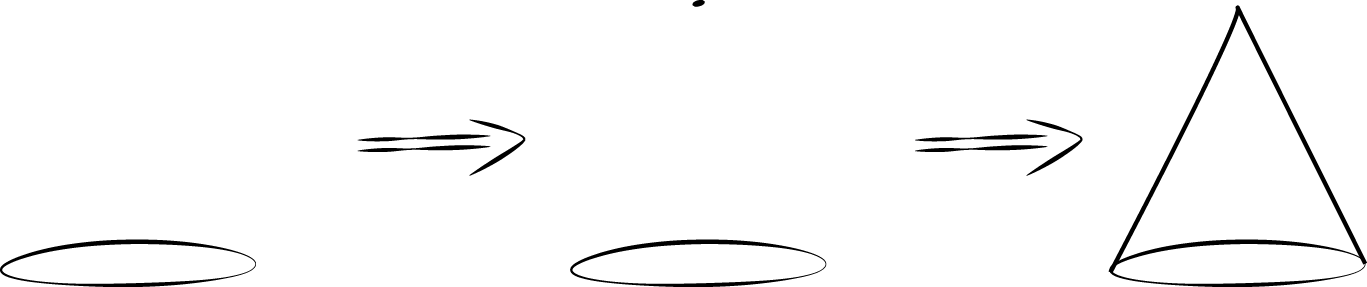
- Draw an oval.
- Draw a point centered above the oval.
- Connect the edges of the oval to the point.
- Which parts of your drawing would be hidden behind the object? Make these parts dashed lines.
- The cylinder has a larger volume.
- Answers vary.
- Answers vary.
 ACTIVITY: 20 minutes15.2: From Cylinders to ConesInstructional RoutinesCCSS Standards: AddressingIn this activity, students use the relationship that the volume of a cone is 13 of the volume of a cylinder to calculate the volume of various cones. Students start by watching a video (or demonstration) that shows that it takes the contents of 3 cones to fill the cylinder when they have congruent bases and equal heights. Students use this information to calculate the volume of various cones and cylinders. For the last question, identify students who:
ACTIVITY: 20 minutes15.2: From Cylinders to ConesInstructional RoutinesCCSS Standards: AddressingIn this activity, students use the relationship that the volume of a cone is 13 of the volume of a cylinder to calculate the volume of various cones. Students start by watching a video (or demonstration) that shows that it takes the contents of 3 cones to fill the cylinder when they have congruent bases and equal heights. Students use this information to calculate the volume of various cones and cylinders. For the last question, identify students who:- write the equation as 13V (or V÷3), where V represents the volume of a cylinder with the same base and height as the cone.
- write the equation in terms of r and h (V=13πr2h ).
 A cone and cylinder have the same height and their bases are congruent circles.
A cone and cylinder have the same height and their bases are congruent circles.- If the volume of the cylinder is 90 cm3, what is the volume of the cone?
- If the volume of the cone is 120 cm3, what is the volume of the cylinder?
- If the volume of the cylinder is V=πr2h, what is the volume of the cone? Either write an expression for the cone or explain the relationship in words.
- 30 cm3. The volume of a cone is 13 the volume of a cylinder and 13⋅90.
- 360 cm3. The volume of the cylinder is 3 times larger than the volume of a cone and 3⋅120.
- Answers vary. Sample responses: V=13πr2h (or equivalent) or “the volume of the cone is 13 that of the volume of the cylinder.”
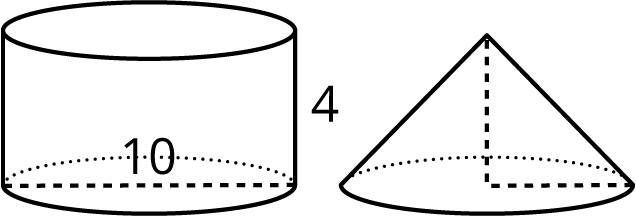
- Here is a cylinder and cone that have the same height and the same base area.What is the volume of each figure? Express your answers in terms of π.
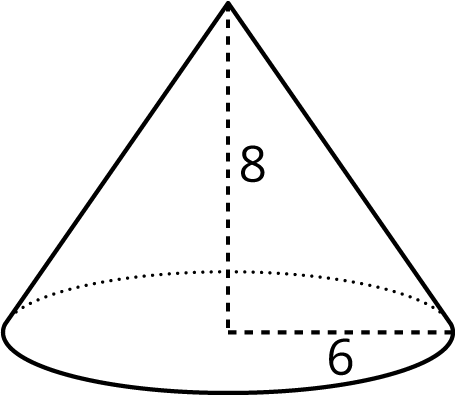
- Here is a cone.
- What is the area of the base? Express your answer in terms of π.
- What is the volume of the cone? Express your answer in terms of π.
- A cone-shaped popcorn cup has a radius of 5 centimeters and a height of 9 centimeters. How many cubic centimeters of popcorn can the cup hold? Use 3.14 as an approximation for π, and give a numerical answer.
- Cylinder: 100π; cone: 1003π. To calculate the volume of the cylinder, find the area of the base and multiply it by the height of the cylinder. The area of the base is πr2, and the height is 4 (π524=100π). The volume of the cone is 13 of the cylinder’s volume, which is 1003π.
- 36π square units because A=π62.
- 96π cubic units because the volume is 13 of the area of the base multiplied by the height of the cone (13⋅36π⋅8=96π).
- 235.5 cm3 because with a radius of 5 cm and a height of 9 cm, the volume is calculated with the equation V=13⋅3.14⋅52⋅9.
 "Are you ready for more?" Student ResponseThe entire grain silo holds 6403π cubic feet of grain.The cone holds 643π cubic feet of grain. Since the radius is 4 feet and the height of the cone is also 4 feet (16−12), the volume is 13π42⋅4. Calculate the volume of the cylinder (π42⋅12), and add it to the volume of the cone to get the volume of the entire silo. Activity SynthesisFor the first problem, Invite students to explain how they calculated the volume of both figures and have them share the different strategies they used. If not mentioned by students bring up these strategies:
"Are you ready for more?" Student ResponseThe entire grain silo holds 6403π cubic feet of grain.The cone holds 643π cubic feet of grain. Since the radius is 4 feet and the height of the cone is also 4 feet (16−12), the volume is 13π42⋅4. Calculate the volume of the cylinder (π42⋅12), and add it to the volume of the cone to get the volume of the entire silo. Activity SynthesisFor the first problem, Invite students to explain how they calculated the volume of both figures and have them share the different strategies they used. If not mentioned by students bring up these strategies:- Calculate the volume of the cylinder, then divide volume of cylinder by 3 to get the volume of the cone.
- Calculate the volume of the cylinder, then multiply volume of cylinder by 13 to get the volume of the cone.
- Calculate the volume of the cone, then multiply volume of cone by 3 to get the volume of the cylinder.
- “What is the relationship between the volume of a cylinder and the volume of a cone?” (The volume of a cone is 13 of the volume of a cylinder or the volume of the cylinder is 3 times the volume of the cone.)
- “If we know the volume of a cone, how do we calculate the volume of a cylinder that has the same height and base area?” (We can multiply the volume of the cone by 3.)
- “If we know the volume of a cylinder, how do we calculate the volume of a cone that has the same height and base area?” (We can multiply the volume of the cylinder by 13.)
- “If a cylinder and a cone have the same base, how tall does the cone have to be relative to the cylinder so that they both have the same volume?” (The cone needs to have a height 3 times the height of the cylinder for the two shapes to have the same volume.)
 Student Responsecylinder: 36π cubic units because π⋅32⋅4=36πcone: 36π cubic units because 13π⋅32⋅12=36π
Student Responsecylinder: 36π cubic units because π⋅32⋅4=36πcone: 36π cubic units because 13π⋅32⋅12=36π