Sinus und Cosinus am Einheitskreis
Wiederholung
Um Sinus, Cosinus und Tangens auch für Winkel definieren zu können, die größer sind als 90° sind, verwendet man den Einheitskreis.
Was ist der Einheitskreis?
Darunter versteht man einen Kreis mit dem Radius von 1. Manchmal zeichnet man sich noch ein Koordinatensystem ein. Der Ursprung dieses Koordinatensystems fällt mit dem Mittelpunkt des Kreises zusammen. Ein Einheitskreis sieht so aus:
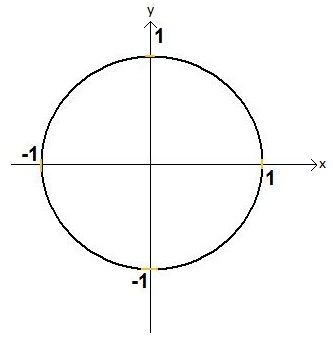Wählt man nun einen beliebigen Punkt P auf dem Einheitskreis, so entsteht ein rechtwinkliges Dreieck, wobei der rechte Winkel immer an der x-Achse liegt und die Hypotenuse immer aus dem Radius des Einheitskreises gebildet wird.
Wählt man nun einen beliebigen Punkt P auf dem Einheitskreis, so entsteht ein rechtwinkliges Dreieck, wobei der rechte Winkel immer an der x-Achse liegt und die Hypotenuse immer aus dem Radius des Einheitskreises gebildet wird.
Den Winkel, den der Radius mit der x-Achse (gegen den Uhrzeigersinn gemessen) einschließt, nennen wir .
Die Strecke BC ist dann die Gegenkathete von und die Strecke AB ist die Ankathete von . Die Hypotenuse ist ja der Radius selbst, er besitzt die Länge 1.
Da das Ergebnis, wenn man eine Zahl durch 1 teilt, immer die Zahl selbst ist, ist =BC und =AC.
Klicke auf die Kästchen und lass dir den Sinus und den Kosinus des Winkels anzeigen.
Sinus und Cosinus am Einheitskreis
An den Koordinaten von P lässt sich also sofort ablesen:
Auf diese Weise kannst du nun auch den Sinus und Kosinus von Winkeln größer als 90° bestimmen:
Lass den Punkt P auf dem Einheitskreis entlanglaufen. Es entstehen immer rechtwinklige Dreiecke. Lass dir jeweils Sinus und Kosinus anzeigen und überprüfe, wie sich der Wert für SInus bzw. Kosinus verändert.
Ergebnisse
Notiere deine Beobachtung in der Tabelle in Aufgabe 4 von Arbeitsblatt M2:
Sicherung
Bearbeite Aufgabe 5 auf dem Arbeitsblatt M2.