Chords of a parabola
Apollonius of Perga (c. 240- 190 BCE) was a Greek mathematician best known for his work on conic sections: parabolas, ellipses, and hyperbolas. This mathematics was considered the pinnacle of mathematical achievement until the 1600s (CE), when new work began exploding in Europe with the adoption of algebra (developed in the Islamic world). Much of Apollonius’s work is unknown today. Here is one theorem.
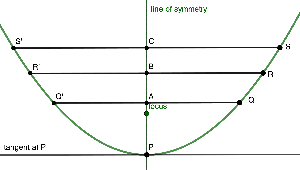
Take any parabola (such as one constructed from a focus and directrix). Choose any point P on the parabola and consider its tangent. (The tangent line comes from the focus-directrix construction; no calculus needed. For a point Q on the parabola, intersect the line through Q parallel to the tangent with the parabola, giving the other endpoint Q’ of the chord.
The midpoints of all such chords are collinear. This line (called a “diameter” of the parabola) is parallel to the line of symmetry of the parabola.
You can move the points P, Q, R, S, the focus, and the points determining the directrix.
This result should remind you of the special case in the picture below, where the x axis is the tangent.