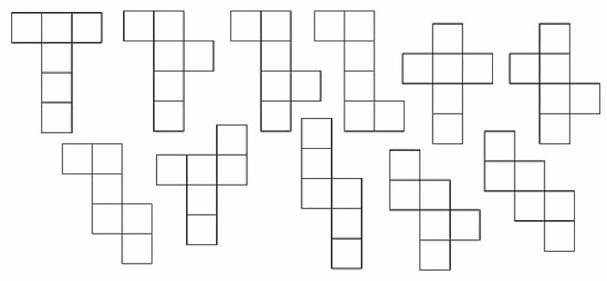
A kocka 11 hálója másolata
A kocka 11 hálója
A feladat: Hány különböző módon teríthető ki a kocka?
Klasszikus ‑akár az általános iskola alsó tagozatában is felvethető ‑ térszemlélet
fejlesztő feladat. Bár a világháló sok helyen „közli”, hogy a feladatnak pontosan 11 megoldása van, matematikai (oktatási - tanulási) szempontból fontos kérdés: hogyan tudnánk belátni, hogy a problémának pontosan ezek a megoldásai, több nincs. E kérdésekre most nem térünk ki. Nem foglalkozunk azzal a kérdéssel sem, hogy mit értünk egy kocka – általában egy poliéder ‑ síkba terítésén, amit szokás az adott poliéder (egy lehetséges) hálójának,olykor hálózatának is nevezni.
A probléma szemléltetése matematikai szempontból nem jelent különösebb nehézséget,
számítástechnikai szempontból azonban komoly odafigyelést, sok türelmet igényel. Nem véletlen, hogy alig található az Interneten jól használható demonstráció. Több olyan webhelyis van, ahol adott rajzok, többnyire hexaminók közül kell kiválasztani, hogy melyek lehetnek a kocka hálói. Ezek közül különösen figyelemreméltó az, amely a kitűzött feladathoz animációval kiegészített magyarázatot is ad arra, hogy miért jó, vagy éppen rossz a kérdésre adott válasz.
Olyan interaktív GeoGebra demonstráció is található, amely arra vállalkozik, hogy bemutassa, miként hajtunk össze kockává egy adott hálót, vagy miként terítjük ki a kockafelületet. Ennek a demonstrációnak az az egyetlen érdeme, hogy még 2012-ben készült, a GeoGebra 3.2-es változatával. Így a szerzőnek meg kellett (volna) oldania a térbeli szituáció helyes dinamikus
ábrázolását.
Bár ebben a munkában a kezdő (kocka) állapot és végeredmény (háló) rajza valóban helyes,
„mozgás” közben több esetben deformálódik egy-egy négyzet, olykor nem is egy síkban fekvő négy pontból álló alakzattá. Így is több mint százezren megnézték, több mint százan „lájkolták” a fájlt, mi több, letöltötték, változatlanul, vagy némi (főként nyelvi) átírást követően újból megosztották a GeoGebra Tube –on, így most legalább hat különböző helyről tölthető le. A dicsérő kommentek
mellett valaki szóvá tette, hogy két kiterítés kétszer is szerepel, így másik két lehetséges eset lemaradt, de a szerző nem akarta kijavítani (ezt) a hibát. A felületes szemlélő számára megnyugtató módon „ott van” a köztudottan 11 megoldás. Az igazi szakmai hibát senki nem vette észre, vagy nem vette komolyan.
„Jót, s jól! Ebben áll a nagy titok.” Az idézet folytatását olvasóinkra bízzuk.
Remélhetőleg sikerült rávilágítani a Geogebra-Tube legnagyobbhátrányára: nem mindíg megbízható. Bárkinek joga van minden kontroll nélkül bármilyen munkát feltenni a világméretű faliújságra, ahol azután – amennyiben maga a téma érdeklődésre tarthat számot – futótűzként el is terjed. Ne is részletezzük a következményeket.
Ez motiválta e sorok íróját arra, hogy mutasson néhány megjelenítésében egymástól alig különböző megoldást a problémára. A GeoGebra fájlok elkészítése iránt érdeklődő olvasóinknak javasoljuk a téma forrásfájljainak a letöltését, alapos elemzését.
Manapság a GeoGebra 3D eszköztárával jóval könnyebb előállítani egy szakmailag korrekt
demonstrációt. Lényegében a Forgatás[<Alakzat>,<Szög>,<Forgatásitengely>]parancsot kellett több, egymásba épített eljárásban alkalmazni.
Itt (1A) a kocka ‑ nem mozgó ‑ éleit tekintettük a forgatás tengelyeinek, így egy-egy pont mozgását legfeljebb három derékszögű forgatás szorzataként kaptuk meg. A geometriai transzformációk szorzatán azok egymás utáni – jelen esetben egymásba ágyazott – végrehajtását érjük.
Pl.: a G_{h,i,a}=Forgatás[Forgatás[Forgatás[G,α,h],α,i],α,a] paranccsal a kocka G pontja a kiterítés során a kockah, i, és a tengelye körül fordul el 90°-os szöggel. Ez a három mozgás egyszerre következik be, így a G pont egy bonyolult térgörbét ír le, miközben az α szög 0°és 90° között változik. Erről meggyőződhetünk, ha kirajzoltatjuk a kiszemelt pont nyomvonalát. Itt jegyezzük meg, hogy a 3D-s rajzérben nyomvonalként leírt görbe megmarad, ha a koordináta-rendszert mozgatjuk, így egy-egy pont útja alaposan szemügyre vehető.
Elegendő a forgatás szögét a 0°≤α≤180° tartományra kiterjesztenünk ahhoz, hogy szemléltessük:
a kiterített háló mindkét féltérbe összehajtható kockává. (1B)
A (2) fájl abban tér el az előzőektől, hogy a mozgást itt fázisokra bontottuk, így könnyebben nyomon követhetők a 90°-os forgások. Ez azt is jelenti, hogy itt egy-egy pont a kiterítés közben valóban negyed körívekből álló pályát ír le.
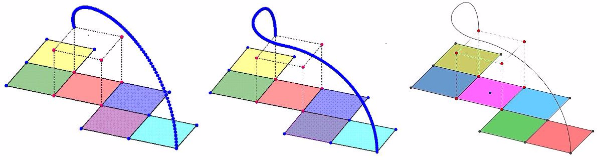
Annak is megvan az előnye, hogy a Geogebra 3D eszköztárát mellőzve csupán síkgeometriai számításokat alkalmazva oldjuk meg a feladatot. (3)
Ezzel finomabb felbontású rajz állítható elő, mértani helyként is kijelölhető egy-egy pont pályája és … ‑ lássuk be ‑ ez sem megoldhatatlanul nehéz feladat.