G 05 Gömbi parketták
Lehetőségek a gömb kiparkettázására.
Egy sík parkettázásán (kövezésén) egybevágó sikidomokkal történő egyrétegű lefedését értjük.Ez azt jeleni, hogy a sík minden belső pontja pontosan egy, a határvonalra illeszkedő pontok pontosan kettő, a határvonalak metszéspontjaira véges sok parkettához tartozhat.
Az euklideszi sík kiparkettázására sokféle síkidom alkalmas. Pl. bármely háromszög bármely négyszög -a konkávokat is beleértve megfelelő. Ha szűkítjük a kört, és csak olyan derékszögű háromszög parkettákat keresünk, ahol a szomszédos háromszögek egymás tükörképei a közös oldalegyenesükre, akkor hamar kiderül, hogy erre csak a 30°, 60°-os, ill. a 45°-os derékszögű háromszög alkalmas.
Itt láthattuk, hogy a hiperbolikus sík kiparkettázására - még a fenti feltételek mellett is - végtelen sok lehetőségünk van.
Ugyanezekkel a feltételekkel hányféleképpen parkettázgató ki a gömb? Mivel a megfelelő háromszög egyik szöge derékszög, a másik kettőre teljesülnie kell annak, hogy mindkettőnek az egész számú többszöröse 360°, továbbá e két szög összege nagyobb 90°-nál. Könnyen belátható hogy ennek a feltételnek csak a 45°, 60°, 90°-os és a 36°, 60°, 90°-os háromszög felel meg. Megfelelnének még a 2 vagy 3 derékszöget tartalmazó háromszögek is, de ezek az előbbi kettőből előállíthatók.
Itt már említettük , hogy egy gömbháromszög területe a T=( α+β+γ)-180° , továbbá 8 derékszögű szabályos háromszög lefedi a gömböt, a gömb felszine 4π = 720°˛ és a két alkalmas derékszögű gömbháromszög területe (45°+60°+90°)-180° = 15° ill. (36°+60°+90°)-180° = 6° így a gömb teljes lefedéséhez 720°/15°= 48 ill, 720°/6° =120 háromszögre van szükség.
45°, 60°, 90° gömb-parketta és a gömbbe írt poliéderek
A fenti applet alaposabb megismerését, felfedezését olvasóinkra bízzuk.
A parketta csúcsai egy kocka és egy oktaéder csúcsainak az alapgömbre vetítésével nyertük. Ha e két poliéder élei merőlegesen metszik egymást, akkor a metszetük az itt is megjelenő félig szabályos poliéder, az un. kocka-oktaéder (=kuboktaéder). Ennek a köré írt gömbje maga az alapgömb.
Az ilyen szabályos, de különböző sokszögekkel határolt, egybevágó testszögletekkel bíró félig szabályos poliéderek az arkhimédészi testek. Közös tulajdonságuk, hogy van köré irt gömbjük, az összes élt érintő középgömbjük, de beírt gömbjük, amelyet minden lapnak érinteni kellene, nincs.
A fenti appletben bemutattunk egy másik értelemben vett félig szabályos poliédert is, a rombikus dodekaédert, amelynek mind a 12 lapja egybevágó (ezért dodekaéder =12 lapú) de nem szabályos, mivel a lapok rombuszok (ezért rombikus) de a testszögletei szabályosak. Az egy csúcsba befutó szomszédos lapok csúcs- ill. lapszögei szögei ugyanakkorák. A négyélű csúcsait úgy kaphatjuk meg, hogy a kocka (egyben az alapgömb) középpontját rendre tükröztük a kocka lapjaira.
Így a négyélű csúcsai nem illeszkednek a gömbre. Ez a poliéder a Catalan poliéderek körébe tartozik. Elnevezésük nem a katalán néphez, hanem E. Charles Catalan (1814-1894) belga matematikus nevéhez kötődik. E poliéderek közös tulajdonsága, hogy lapjaik egybevágók, testszögleteik szabályosak, (de nem egybevágók), van beírt gömbjük és középgömbjük, de köré írt gömbjük nincs.
A 36°, 60°, 90° -os gömb-parketta származtatása.
Az öt jól ismert szabályos poliéder - a platóni testek - közül a fent látott kocka - oktaéder kapcsolathoz hasonló viszony az un. duális kapcsolat van a dodekaéder és az ikozaéder között.
Az alábbi appletben e kapcsolat helyett inkább arra tettük a hangsúlyt, hogy miként lehet (könnyen? gyorsan?, pontosan?) előállítani azt a 120 egybevágó derékszögű gömb-háromszöget, amellyel ugyancsak kiparkettázható a gömbfelület.
36°, 60°, 90° gömb-parketta és szerkesztése
Ha már itt tartunk ...
... e sorok írója hadd dicsekedjék könyvespolcának egyik féltve őrzött kincsével, amelyet B. M. Sewart -tól (1914-1994) kapott. Ez a kézzel írt és rajzolt - dedikált :-) - könyv nem csak az alábbi rajzot tartalmazza, hanem egy leírást is arról, hogy hogyan kell ennek a konstrukciónak a papírmodelljét elkészíteni.
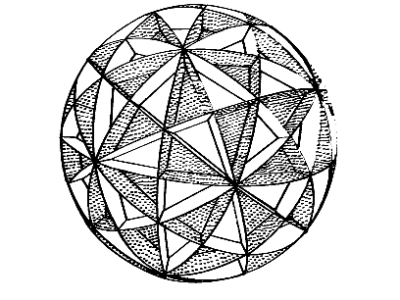
Itt az egyszerű (??) recept:
- Végy egy háromszöget, amelynek az oldalai 4, 6 és 7 cm;
- az oldalaira ( háromszög felé) rajzolj egy-egy 11 cm szárú egyenlő szárú háromszöget;
- ezek csúcsaiból rajzolj az oldalakhoz egy-egy (pl.) 13 cm sugarú körívet, amelynek a végpontjai az egyenlő szárú háromszög szárainak a meghosszabbításaira esnek;
- az így kapott síkidomból készíts ízlés szerint színű és vastagságú papírból kivágott 60 jobbos és 60 balos példányt;
- ezeket hajlítsd meg a háromszögek oldalai mentén, majd ragaszd össze a felhajtott egybevágó körcikk darabokat.
A sablon:
Pontosan?
Ami a pontosságot illeti, viszonylag könnyen ellenőrizhető pl. a fenti 36°,60°,90° os gömbparketta applet letöltött változatával.
Kössük össze egy elemi G-háromszög csúcsait egy-egy (euklideszi értelemben vett) húrral, ezeket nyújtsuk 11/5 arányban. Eredményül ezeket a távolságokat kapjuk: 3.991...≈4 , 6.012...≈6 , 7.049...≈7 .Ez gyakorlatilag több, mint elegendő. Sőt, meglepően jó közelítés.
Aki nem hiszi, járjon utána.
Utána jártunk.
Az alábbi appletben numerikus adatok nélkül állítottuk elő a sablonban használt távolságokat: A GeoGebra CAS eszköztára képletekkel számol, kerekítés nélkül (helyettünk) :
Egy kis kiegészítés:
- 1. t: Mint az appletben láttuk a dodekaéder és az ikozaéder csúcsainak a megadásához az aranymetszés aránya elengedhetetlenül szükséges.
- 2. A: dodekaéder egyik csúcsa.
- 3. r: Az A csúcs távolsága a dodekaéder köré írt gömb középpontjától. Nem meglepő a kapott eredmény, a dodekaéder csúcsai között a 2 egységnyi élű kocka csúcsai is ott vannak.
- 4.-5. BT , d : A t-vel előállított ikozaéder és dodekaéder köré írt gömb sugara nem egyenlő.
- 6. -7 B, k : Most már A és B ugyabarra a gömbre illeszkedik, k -val ellenőriztük.
- 8. A C pont a z tengelyre illeszkedik.
- 9.-14: Megkaptuk az ABC Δ oldalait egy egy algebrai kifejezés formájában. a 11 sugarú gömbre kivetítve is.
- 12.-16: Ugyanezeket megkaptuk 10^(-10) pontossággal is.