Dedução da fórmula do Volume da esfera

Autor:: Jorge Cássio

Tópico:: Esfera, Volume

Movimente o controle deslizante "Etapas" e marque as caixas de Esconder/Mostrar

Reflexão

Clique com o botão direito do mouse, segure e arraste a janela 3d. Olhe a anticlepsidra em diferentes posições. Ela se parece com algum objeto que você conhece?

Áreas das secções

Reflexão 2

Movimente o ponto R para alterar a posição do plano. Compare as medidas das áreas da coroa circular e do círculo. O que você percebe?

Justificativa?

Para justificarmos a propriedade anterior, precisamos verificar outra.

Raio do círculo menor da coroa e distância do centro ao vértice do Cone

Reflexão 3

Na construção anterior, compare a medida do raio do círculo menor da coroa com a distância de seu centro ao vértice. O que você observa? Altere a posição do ponto R para movimentar o plano. O que você observa?

Exercício-Justificativa

Utilize a figura seguinte para justificar a propriedade vista anteriormente. Use semelhança de triângulos para mostrar que o raio do círculo menor da coroa é igual a distância de seu centro ao vértice. Lembre-se que a altura do cone é igual ao raio da base.

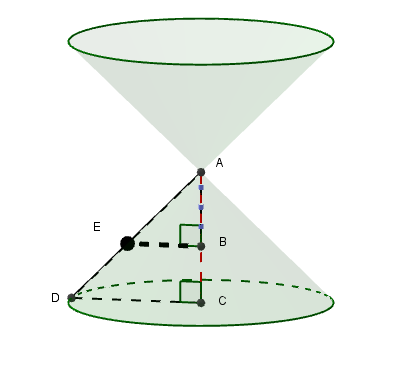
Justificativa para as secções com mesma área

Reflexão 1

Entendeu a demonstração? Desmarque as caixas "Exibir/Esconder" para visualizar melhor as atividades.

Volume da anticlepsidra

Mostramos que as medidas das áreas das secções formadas na anticlepsidra e na esfera são iguais. Como a altura da anticlepsidra é igual ao diâmetro da esfera, então pelo princípio de Cavalieri, possuem volumes iguais. Dessa forma, basta calcular o volume da anticlepsidra. Para isso, precisamos calcular o volume do cilindro e subtrair o volume dos dois cones.