ES 37.22
Given points A,B,C,O with O,A,B not collinear, construct the intersection points of the line AB with the circle with center O and passing by C (assuming that they meet) (par = 4 steps, done in 3).
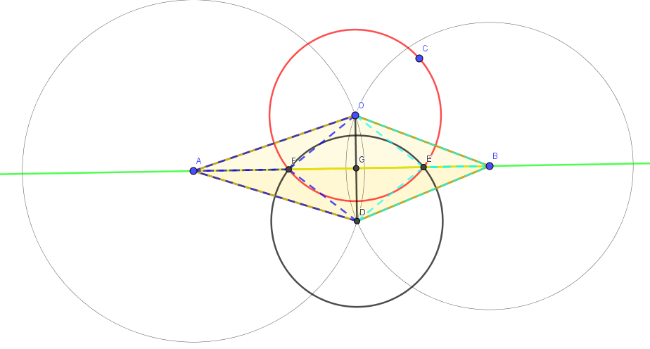
PROCEDURA.
Sia c la circonferenza di partenza, di centro O, e A, B i punti che definiscono la retta.
-Traccio la circonferenza di centro A e raggio AO, a. {1 STEP}
-Traccio la circonferenza di centro B e raggio BO, b. {1 STEP}
-Sia D l'altro punto di intersezione delle circonferenze a, b.
-Traccio la circonferenza di centro D e raggio CO, d. {1 STEP}
-I punti di intersezione delle circonferenze c e d mi restituiscono i punti di intersezione della retta per A, B con c, ovvero: E, F.
TOT: 3 STEP
DIMOSTRAZIONE.
In riferimento a quanto scritto sopra e alla figura in basso, abbiamo che le circonferenze a e b si intersecano in due punti: O (per costruzione) e D (infatti per ipotesi A, O, B non sono allineati e quindi le due circonferenze non possono essere tangenti).
Siano F, E i punti di intersezione della retta AB con la circonferenza c, voglio mostrare che questi punti appartengono anche a d.
Considero i triangoli AOB, ADB: sono congruenti per LLL, infatti: AO=AD perchè raggi della circonferenza a, AB=BD perchè raggi della circonferenza b e AB è in comune.
In particolare gli angoli OAB=BAD.
Traccio il segmento OD: questo interseca necessariamente AB per il Crossbar su AOB. Sia G il punto di intersezione.
Considero i triangoli OAF e DAF, sono congruenti per LAL infatti OA=AD, AF in comune e gli angoli in A sono congruenti per quanto detto sopra. In particolare, DF=OF.
Ma allora DF=OF=OC.
Analogamente si può trovare che OC=OE=ED. Per la transitività della relazione di congruenza segue che FD=ED.Quindi la circonferenza di centro D e raggio OC interseca la retta AB in F e E.